Computational role of eccentricity dependent cortical magnification
Paper and Code
Jun 06, 2014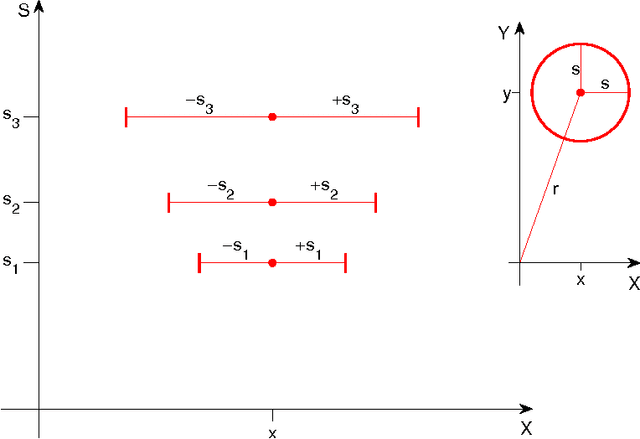
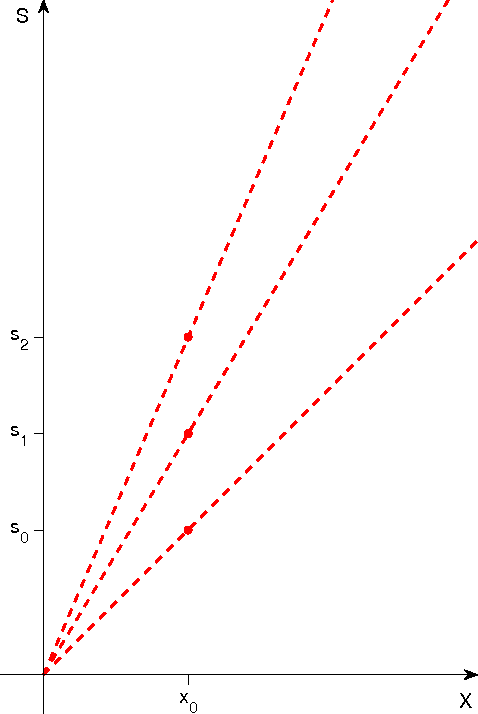
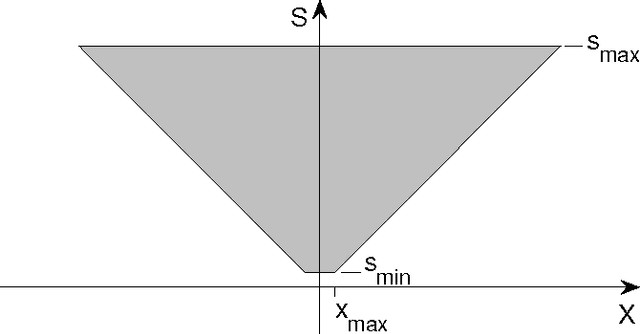
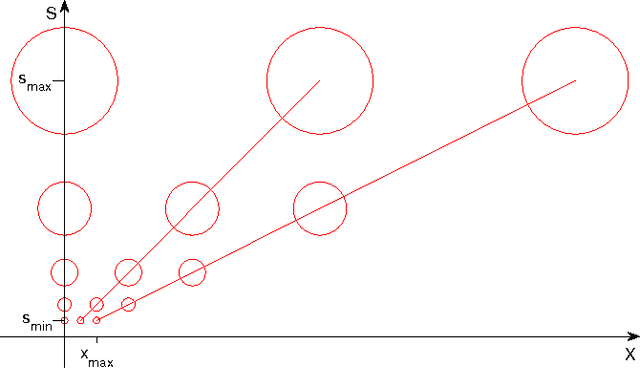
We develop a sampling extension of M-theory focused on invariance to scale and translation. Quite surprisingly, the theory predicts an architecture of early vision with increasing receptive field sizes and a high resolution fovea -- in agreement with data about the cortical magnification factor, V1 and the retina. From the slope of the inverse of the magnification factor, M-theory predicts a cortical "fovea" in V1 in the order of $40$ by $40$ basic units at each receptive field size -- corresponding to a foveola of size around $26$ minutes of arc at the highest resolution, $\approx 6$ degrees at the lowest resolution. It also predicts uniform scale invariance over a fixed range of scales independently of eccentricity, while translation invariance should depend linearly on spatial frequency. Bouma's law of crowding follows in the theory as an effect of cortical area-by-cortical area pooling; the Bouma constant is the value expected if the signature responsible for recognition in the crowding experiments originates in V2. From a broader perspective, the emerging picture suggests that visual recognition under natural conditions takes place by composing information from a set of fixations, with each fixation providing recognition from a space-scale image fragment -- that is an image patch represented at a set of increasing sizes and decreasing resolutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge