Unsupervised detection of semantic correlations in big data

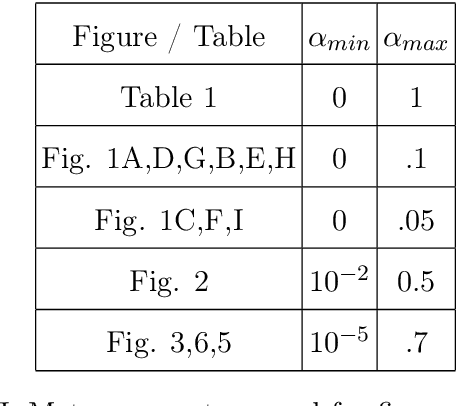
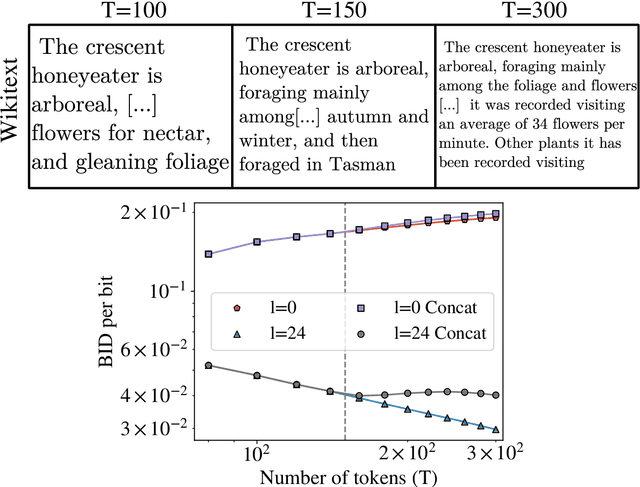
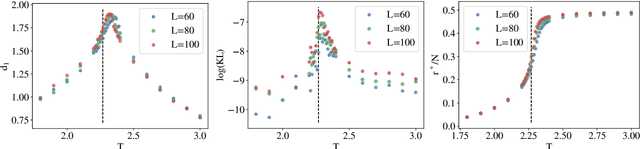
In real-world data, information is stored in extremely large feature vectors. These variables are typically correlated due to complex interactions involving many features simultaneously. Such correlations qualitatively correspond to semantic roles and are naturally recognized by both the human brain and artificial neural networks. This recognition enables, for instance, the prediction of missing parts of an image or text based on their context. We present a method to detect these correlations in high-dimensional data represented as binary numbers. We estimate the binary intrinsic dimension of a dataset, which quantifies the minimum number of independent coordinates needed to describe the data, and is therefore a proxy of semantic complexity. The proposed algorithm is largely insensitive to the so-called curse of dimensionality, and can therefore be used in big data analysis. We test this approach identifying phase transitions in model magnetic systems and we then apply it to the detection of semantic correlations of images and text inside deep neural networks.

Density Estimation via Binless Multidimensional Integration

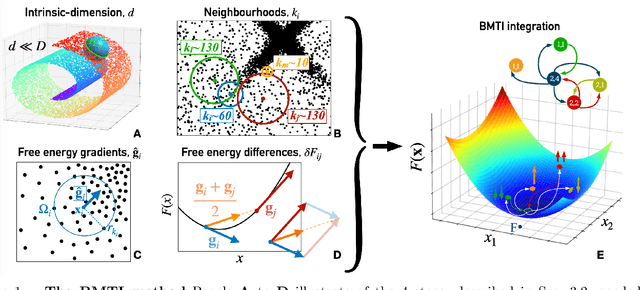
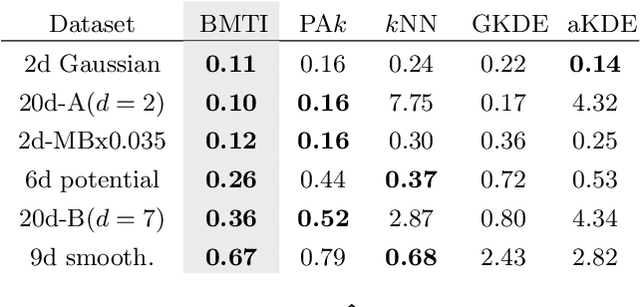
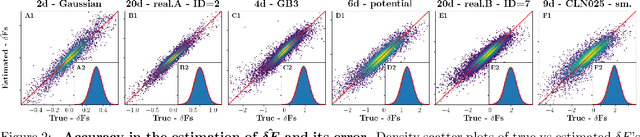
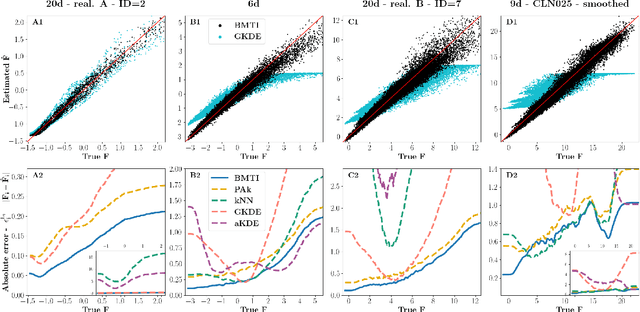
We introduce the Binless Multidimensional Thermodynamic Integration (BMTI) method for nonparametric, robust, and data-efficient density estimation. BMTI estimates the logarithm of the density by initially computing log-density differences between neighbouring data points. Subsequently, such differences are integrated, weighted by their associated uncertainties, using a maximum-likelihood formulation. This procedure can be seen as an extension to a multidimensional setting of the thermodynamic integration, a technique developed in statistical physics. The method leverages the manifold hypothesis, estimating quantities within the intrinsic data manifold without defining an explicit coordinate map. It does not rely on any binning or space partitioning, but rather on the construction of a neighbourhood graph based on an adaptive bandwidth selection procedure. BMTI mitigates the limitations commonly associated with traditional nonparametric density estimators, effectively reconstructing smooth profiles even in high-dimensional embedding spaces. The method is tested on a variety of complex synthetic high-dimensional datasets, where it is shown to outperform traditional estimators, and is benchmarked on realistic datasets from the chemical physics literature.

Intrinsic Dimension Correlation: uncovering nonlinear connections in multimodal representations

To gain insight into the mechanisms behind machine learning methods, it is crucial to establish connections among the features describing data points. However, these correlations often exhibit a high-dimensional and strongly nonlinear nature, which makes them challenging to detect using standard methods. This paper exploits the entanglement between intrinsic dimensionality and correlation to propose a metric that quantifies the (potentially nonlinear) correlation between high-dimensional manifolds. We first validate our method on synthetic data in controlled environments, showcasing its advantages and drawbacks compared to existing techniques. Subsequently, we extend our analysis to large-scale applications in neural network representations. Specifically, we focus on latent representations of multimodal data, uncovering clear correlations between paired visual and textual embeddings, whereas existing methods struggle significantly in detecting similarity. Our results indicate the presence of highly nonlinear correlation patterns between latent manifolds.

Can you trust your explanations? A robustness test for feature attribution methods

The increase of legislative concerns towards the usage of Artificial Intelligence (AI) has recently led to a series of regulations striving for a more transparent, trustworthy and accountable AI. Along with these proposals, the field of Explainable AI (XAI) has seen a rapid growth but the usage of its techniques has at times led to unexpected results. The robustness of the approaches is, in fact, a key property often overlooked: it is necessary to evaluate the stability of an explanation (to random and adversarial perturbations) to ensure that the results are trustable. To this end, we propose a test to evaluate the robustness to non-adversarial perturbations and an ensemble approach to analyse more in depth the robustness of XAI methods applied to neural networks and tabular datasets. We will show how leveraging manifold hypothesis and ensemble approaches can be beneficial to an in-depth analysis of the robustness.

Relating Implicit Bias and Adversarial Attacks through Intrinsic Dimension

Despite their impressive performance in classification, neural networks are known to be vulnerable to adversarial attacks. These attacks are small perturbations of the input data designed to fool the model. Naturally, a question arises regarding the potential connection between the architecture, settings, or properties of the model and the nature of the attack. In this work, we aim to shed light on this problem by focusing on the implicit bias of the neural network, which refers to its inherent inclination to favor specific patterns or outcomes. Specifically, we investigate one aspect of the implicit bias, which involves the essential Fourier frequencies required for accurate image classification. We conduct tests to assess the statistical relationship between these frequencies and those necessary for a successful attack. To delve into this relationship, we propose a new method that can uncover non-linear correlations between sets of coordinates, which, in our case, are the aforementioned frequencies. By exploiting the entanglement between intrinsic dimension and correlation, we provide empirical evidence that the network bias in Fourier space and the target frequencies of adversarial attacks are closely tied.

DADApy: Distance-based Analysis of DAta-manifolds in Python

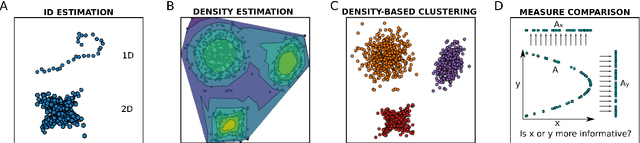
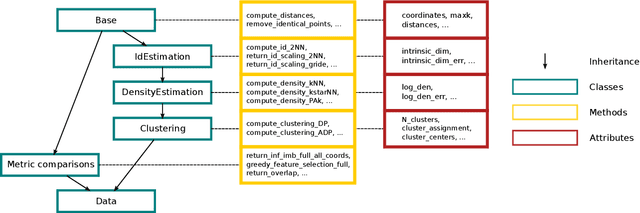
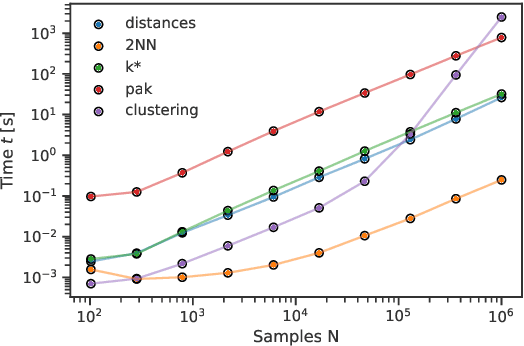
DADApy is a python software package for analysing and characterising high-dimensional data manifolds. It provides methods for estimating the intrinsic dimension and the probability density, for performing density-based clustering and for comparing different distance metrics. We review the main functionalities of the package and exemplify its usage in toy cases and in a real-world application. The package is freely available under the open-source Apache 2.0 license and can be downloaded from the Github page https://github.com/sissa-data-science/DADApy.

Estimating the intrinsic dimension of datasets by a minimal neighborhood information

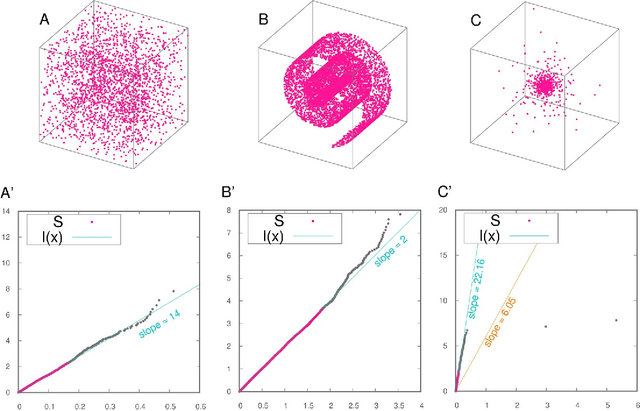
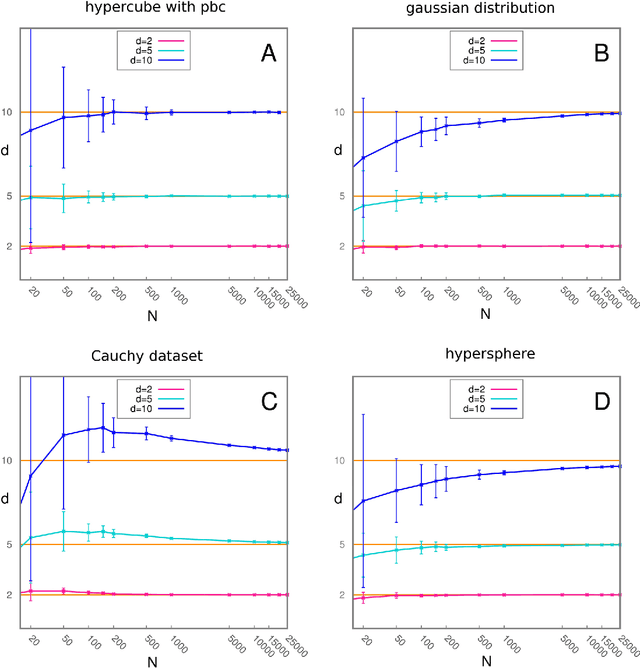
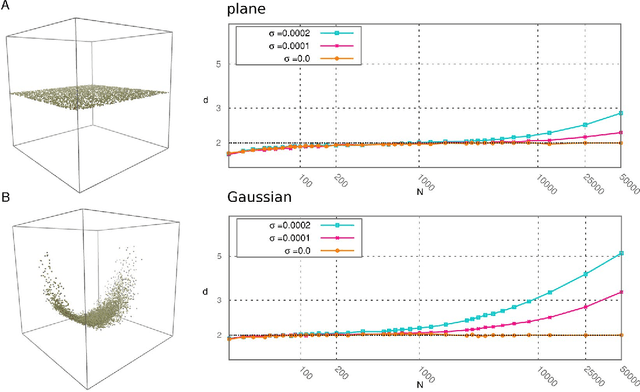
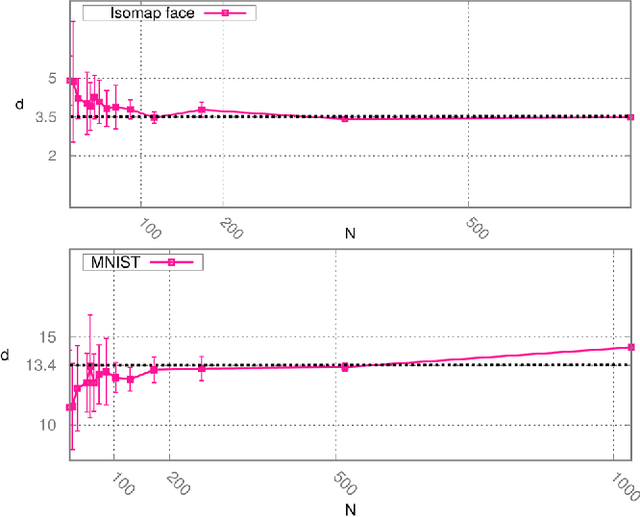
Analyzing large volumes of high-dimensional data is an issue of fundamental importance in data science, molecular simulations and beyond. Several approaches work on the assumption that the important content of a dataset belongs to a manifold whose Intrinsic Dimension (ID) is much lower than the crude large number of coordinates. Such manifold is generally twisted and curved, in addition points on it will be non-uniformly distributed: two factors that make the identification of the ID and its exploitation really hard. Here we propose a new ID estimator using only the distance of the first and the second nearest neighbor of each point in the sample. This extreme minimality enables us to reduce the effects of curvature, of density variation, and the resulting computational cost. The ID estimator is theoretically exact in uniformly distributed datasets, and provides consistent measures in general. When used in combination with block analysis, it allows discriminating the relevant dimensions as a function of the block size. This allows estimating the ID even when the data lie on a manifold perturbed by a high-dimensional noise, a situation often encountered in real world data sets. We demonstrate the usefulness of the approach on molecular simulations and image analysis.

Automatic topography of high-dimensional data sets by non-parametric Density Peak clustering

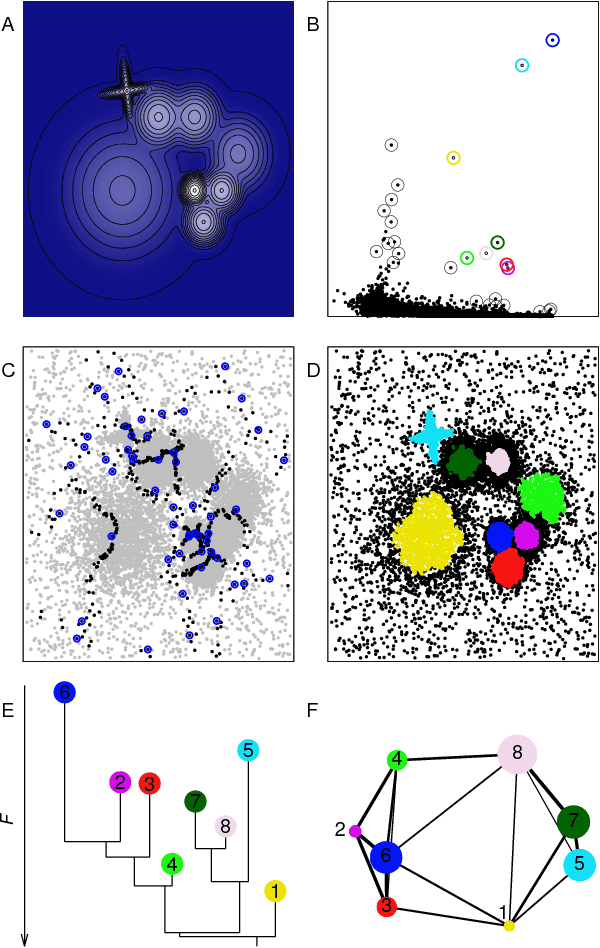
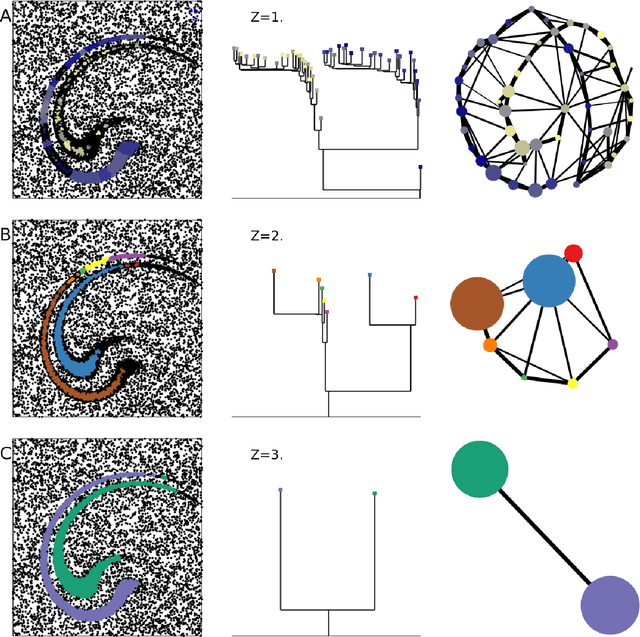
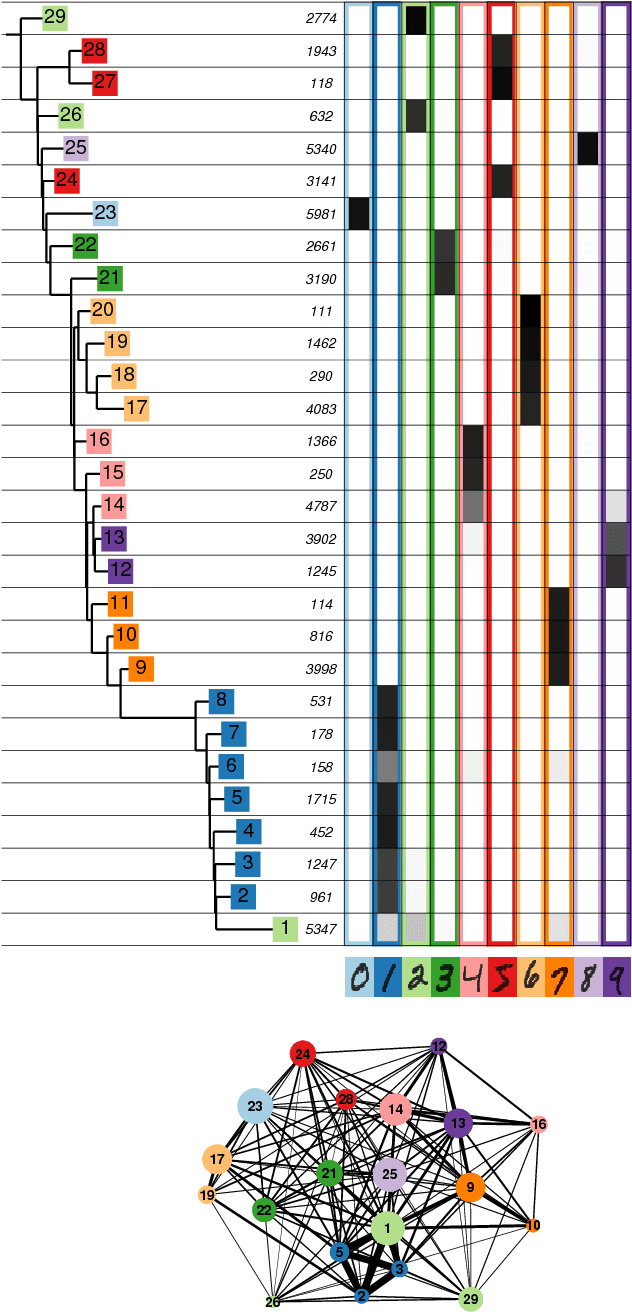
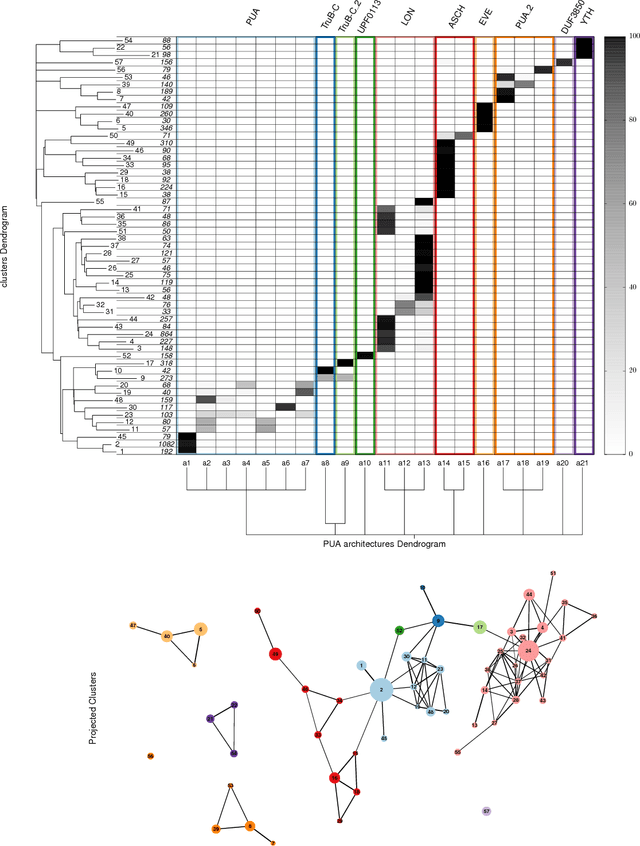
Data analysis in high-dimensional spaces aims at obtaining a synthetic description of a data set, revealing its main structure and its salient features. We here introduce an approach for charting data spaces, providing a topography of the probability distribution from which the data are harvested. This topography includes information on the number and the height of the probability peaks, the depth of the "valleys" separating them, the relative location of the peaks and their hierarchical organization. The topography is reconstructed by using an unsupervised variant of Density Peak clustering exploiting a non-parametric density estimator, which automatically measures the density in the manifold containing the data. Importantly, the density estimator provides an estimate of the error. This is a key feature, which allows distinguishing genuine probability peaks from density fluctuations due to finite sampling.