Differential syntactic and semantic encoding in LLMs

We study how syntactic and semantic information is encoded in inner layer representations of Large Language Models (LLMs), focusing on the very large DeepSeek-V3. We find that, by averaging hidden-representation vectors of sentences sharing syntactic structure or meaning, we obtain vectors that capture a significant proportion of the syntactic and semantic information contained in the representations. In particular, subtracting these syntactic and semantic ``centroids'' from sentence vectors strongly affects their similarity with syntactically and semantically matched sentences, respectively, suggesting that syntax and semantics are, at least partially, linearly encoded. We also find that the cross-layer encoding profiles of syntax and semantics are different, and that the two signals can to some extent be decoupled, suggesting differential encoding of these two types of linguistic information in LLM representations.

An approach to identify the most semantically informative deep representations of text and images

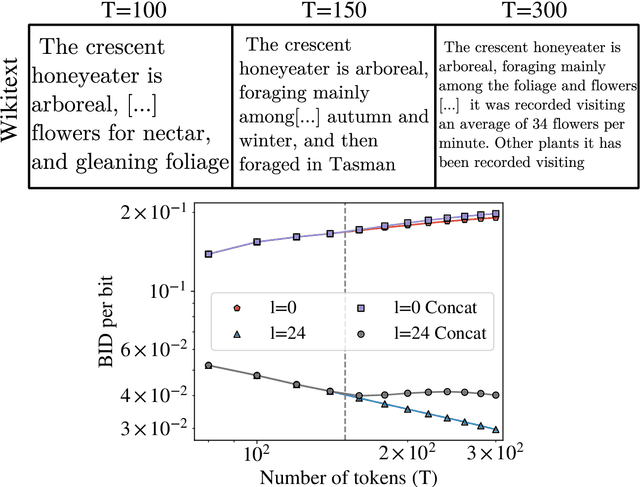
Deep neural networks are known to develop similar representations for semantically related data, even when they belong to different domains, such as an image and its description, or the same text in different languages. We present a method for quantitatively investigating this phenomenon by measuring the relative information content of the representations of semantically related data and probing how it is encoded into multiple tokens of large language models (LLMs) and vision transformers. Looking first at how LLMs process pairs of translated sentences, we identify inner ``semantic'' layers containing the most language-transferable information. We find moreover that, on these layers, a larger LLM (DeepSeek-V3) extracts significantly more general information than a smaller one (Llama3.1-8B). Semantic information is spread across many tokens and it is characterized by long-distance correlations between tokens and by a causal left-to-right (i.e., past-future) asymmetry. We also identify layers encoding semantic information within visual transformers. We show that caption representations in the semantic layers of LLMs predict visual representations of the corresponding images. We observe significant and model-dependent information asymmetries between image and text representations.

Unsupervised detection of semantic correlations in big data

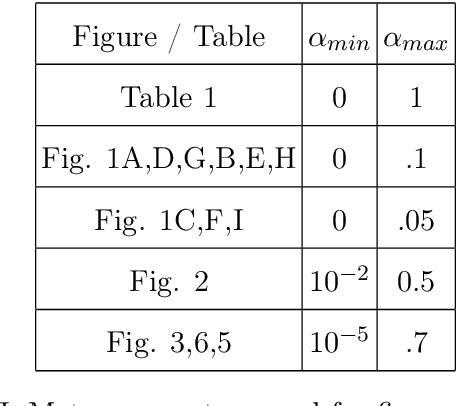
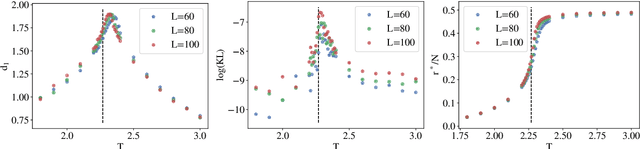
In real-world data, information is stored in extremely large feature vectors. These variables are typically correlated due to complex interactions involving many features simultaneously. Such correlations qualitatively correspond to semantic roles and are naturally recognized by both the human brain and artificial neural networks. This recognition enables, for instance, the prediction of missing parts of an image or text based on their context. We present a method to detect these correlations in high-dimensional data represented as binary numbers. We estimate the binary intrinsic dimension of a dataset, which quantifies the minimum number of independent coordinates needed to describe the data, and is therefore a proxy of semantic complexity. The proposed algorithm is largely insensitive to the so-called curse of dimensionality, and can therefore be used in big data analysis. We test this approach identifying phase transitions in model magnetic systems and we then apply it to the detection of semantic correlations of images and text inside deep neural networks.

Intrinsic Dimension Correlation: uncovering nonlinear connections in multimodal representations

To gain insight into the mechanisms behind machine learning methods, it is crucial to establish connections among the features describing data points. However, these correlations often exhibit a high-dimensional and strongly nonlinear nature, which makes them challenging to detect using standard methods. This paper exploits the entanglement between intrinsic dimensionality and correlation to propose a metric that quantifies the (potentially nonlinear) correlation between high-dimensional manifolds. We first validate our method on synthetic data in controlled environments, showcasing its advantages and drawbacks compared to existing techniques. Subsequently, we extend our analysis to large-scale applications in neural network representations. Specifically, we focus on latent representations of multimodal data, uncovering clear correlations between paired visual and textual embeddings, whereas existing methods struggle significantly in detecting similarity. Our results indicate the presence of highly nonlinear correlation patterns between latent manifolds.