The Narrow Gate: Localized Image-Text Communication in Vision-Language Models

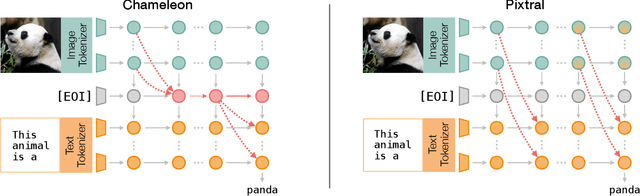
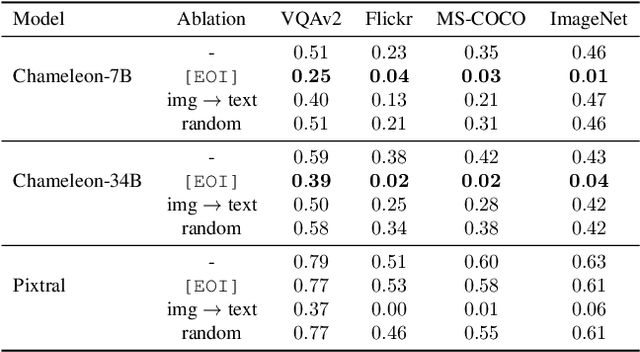
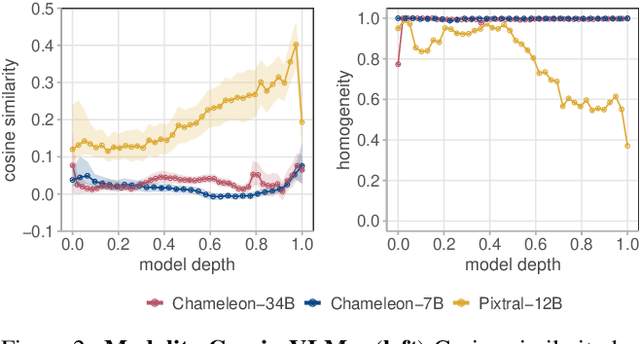
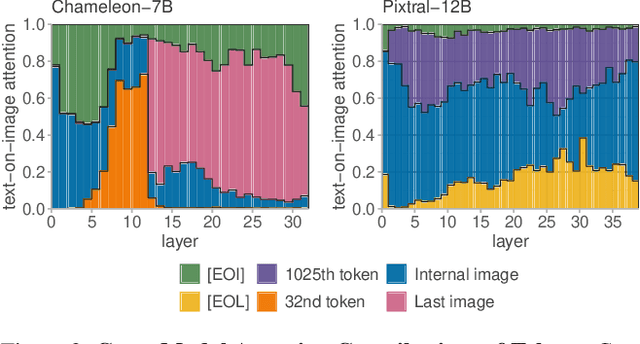
Recent advances in multimodal training have significantly improved the integration of image understanding and generation within a unified model. This study investigates how vision-language models (VLMs) handle image-understanding tasks, specifically focusing on how visual information is processed and transferred to the textual domain. We compare VLMs that generate both images and text with those that output only text, highlighting key differences in information flow. We find that in models with multimodal outputs, image and text embeddings are more separated within the residual stream. Additionally, models vary in how information is exchanged from visual to textual tokens. VLMs that only output text exhibit a distributed communication pattern, where information is exchanged through multiple image tokens. In contrast, models trained for image and text generation rely on a single token that acts as a narrow gate for the visual information. We demonstrate that ablating this single token significantly deteriorates performance on image understanding tasks. Furthermore, modifying this token enables effective steering of the image semantics, showing that targeted, local interventions can reliably control the model's global behavior.

ResiDual Transformer Alignment with Spectral Decomposition

When examined through the lens of their residual streams, a puzzling property emerges in transformer networks: residual contributions (e.g., attention heads) sometimes specialize in specific tasks or input attributes. In this paper, we analyze this phenomenon in vision transformers, focusing on the spectral geometry of residuals, and explore its implications for modality alignment in vision-language models. First, we link it to the intrinsically low-dimensional structure of visual head representations, zooming into their principal components and showing that they encode specialized roles across a wide variety of input data distributions. Then, we analyze the effect of head specialization in multimodal models, focusing on how improved alignment between text and specialized heads impacts zero-shot classification performance. This specialization-performance link consistently holds across diverse pre-training data, network sizes, and objectives, demonstrating a powerful new mechanism for boosting zero-shot classification through targeted alignment. Ultimately, we translate these insights into actionable terms by introducing ResiDual, a technique for spectral alignment of the residual stream. Much like panning for gold, it lets the noise from irrelevant unit principal components (i.e., attributes) wash away to amplify task-relevant ones. Remarkably, this dual perspective on modality alignment yields fine-tuning level performances on different data distributions while modeling an extremely interpretable and parameter-efficient transformation, as we extensively show on more than 50 (pre-trained network, dataset) pairs.

Intrinsic Dimension Correlation: uncovering nonlinear connections in multimodal representations

To gain insight into the mechanisms behind machine learning methods, it is crucial to establish connections among the features describing data points. However, these correlations often exhibit a high-dimensional and strongly nonlinear nature, which makes them challenging to detect using standard methods. This paper exploits the entanglement between intrinsic dimensionality and correlation to propose a metric that quantifies the (potentially nonlinear) correlation between high-dimensional manifolds. We first validate our method on synthetic data in controlled environments, showcasing its advantages and drawbacks compared to existing techniques. Subsequently, we extend our analysis to large-scale applications in neural network representations. Specifically, we focus on latent representations of multimodal data, uncovering clear correlations between paired visual and textual embeddings, whereas existing methods struggle significantly in detecting similarity. Our results indicate the presence of highly nonlinear correlation patterns between latent manifolds.

Scalable unsupervised alignment of general metric and non-metric structures

Aligning data from different domains is a fundamental problem in machine learning with broad applications across very different areas, most notably aligning experimental readouts in single-cell multiomics. Mathematically, this problem can be formulated as the minimization of disagreement of pair-wise quantities such as distances and is related to the Gromov-Hausdorff and Gromov-Wasserstein distances. Computationally, it is a quadratic assignment problem (QAP) that is known to be NP-hard. Prior works attempted to solve the QAP directly with entropic or low-rank regularization on the permutation, which is computationally tractable only for modestly-sized inputs, and encode only limited inductive bias related to the domains being aligned. We consider the alignment of metric structures formulated as a discrete Gromov-Wasserstein problem and instead of solving the QAP directly, we propose to learn a related well-scalable linear assignment problem (LAP) whose solution is also a minimizer of the QAP. We also show a flexible extension of the proposed framework to general non-metric dissimilarities through differentiable ranks. We extensively evaluate our approach on synthetic and real datasets from single-cell multiomics and neural latent spaces, achieving state-of-the-art performance while being conceptually and computationally simple.

Emergent representations in networks trained with the Forward-Forward algorithm

The Backpropagation algorithm, widely used to train neural networks, has often been criticised for its lack of biological realism. In an attempt to find a more biologically plausible alternative, and avoid to back-propagate gradients in favour of using local learning rules, the recently introduced Forward-Forward algorithm replaces the traditional forward and backward passes of Backpropagation with two forward passes. In this work, we show that internal representations obtained with the Forward-Forward algorithm organize into robust, category-specific ensembles, composed by an extremely low number of active units (high sparsity). This is remarkably similar to what is observed in cortical representations during sensory processing. While not found in models trained with standard Backpropagation, sparsity emerges also in networks optimized by Backpropagation, on the same training objective of Forward-Forward. These results suggest that the learning procedure proposed by Forward-Forward may be superior to Backpropagation in modelling learning in the cortex, even when a backward pass is used.

Relating Implicit Bias and Adversarial Attacks through Intrinsic Dimension

Despite their impressive performance in classification, neural networks are known to be vulnerable to adversarial attacks. These attacks are small perturbations of the input data designed to fool the model. Naturally, a question arises regarding the potential connection between the architecture, settings, or properties of the model and the nature of the attack. In this work, we aim to shed light on this problem by focusing on the implicit bias of the neural network, which refers to its inherent inclination to favor specific patterns or outcomes. Specifically, we investigate one aspect of the implicit bias, which involves the essential Fourier frequencies required for accurate image classification. We conduct tests to assess the statistical relationship between these frequencies and those necessary for a successful attack. To delve into this relationship, we propose a new method that can uncover non-linear correlations between sets of coordinates, which, in our case, are the aforementioned frequencies. By exploiting the entanglement between intrinsic dimension and correlation, we provide empirical evidence that the network bias in Fourier space and the target frequencies of adversarial attacks are closely tied.