Implicit bias as a Gauge correction: Theory and Inverse Design

A central problem in machine learning theory is to characterize how learning dynamics select particular solutions among the many compatible with the training objective, a phenomenon, called implicit bias, which remains only partially characterized. In the present work, we identify a general mechanism, in terms of an explicit geometric correction of the learning dynamics, for the emergence of implicit biases, arising from the interaction between continuous symmetries in the model's parametrization and stochasticity in the optimization process. Our viewpoint is constructive in two complementary directions: given model symmetries, one can derive the implicit bias they induce; conversely, one can inverse-design a wide class of different implicit biases by computing specific redundant parameterizations. More precisely, we show that, when the dynamics is expressed in the quotient space obtained by factoring out the symmetry group of the parameterization, the resulting stochastic differential equation gains a closed form geometric correction in the stationary distribution of the optimizer dynamics favoring orbits with small local volume. We compute the resulting symmetry induced bias for a range of architectures, showing how several well known results fit into a single unified framework. The approach also provides a practical methodology for deriving implicit biases in new settings, and it yields concrete, testable predictions that we confirm by numerical simulations on toy models trained on synthetic data, leaving more complex scenarios for future work. Finally, we test the implicit bias inverse-design procedure in notable cases, including biases toward sparsity in linear features or in spectral properties of the model parameters.

Interpreting and Steering Protein Language Models through Sparse Autoencoders

The rapid advancements in transformer-based language models have revolutionized natural language processing, yet understanding the internal mechanisms of these models remains a significant challenge. This paper explores the application of sparse autoencoders (SAE) to interpret the internal representations of protein language models, specifically focusing on the ESM-2 8M parameter model. By performing a statistical analysis on each latent component's relevance to distinct protein annotations, we identify potential interpretations linked to various protein characteristics, including transmembrane regions, binding sites, and specialized motifs. We then leverage these insights to guide sequence generation, shortlisting the relevant latent components that can steer the model towards desired targets such as zinc finger domains. This work contributes to the emerging field of mechanistic interpretability in biological sequence models, offering new perspectives on model steering for sequence design.

The Narrow Gate: Localized Image-Text Communication in Vision-Language Models

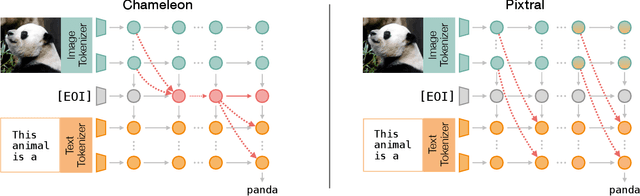
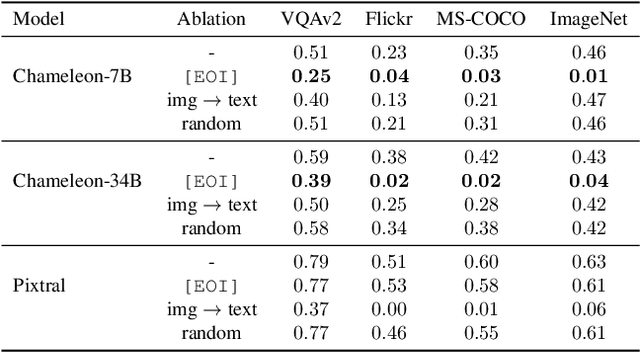
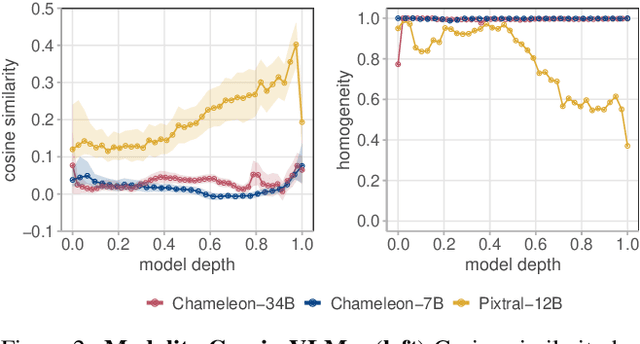
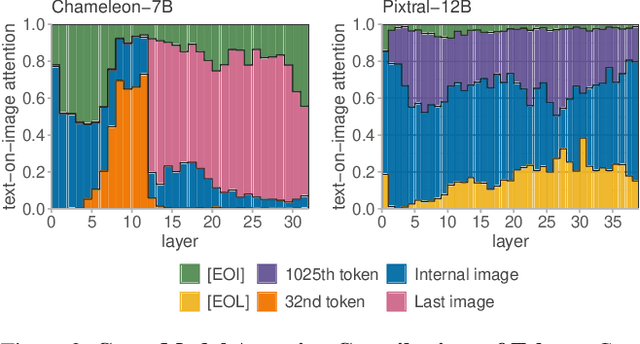
Recent advances in multimodal training have significantly improved the integration of image understanding and generation within a unified model. This study investigates how vision-language models (VLMs) handle image-understanding tasks, specifically focusing on how visual information is processed and transferred to the textual domain. We compare VLMs that generate both images and text with those that output only text, highlighting key differences in information flow. We find that in models with multimodal outputs, image and text embeddings are more separated within the residual stream. Additionally, models vary in how information is exchanged from visual to textual tokens. VLMs that only output text exhibit a distributed communication pattern, where information is exchanged through multiple image tokens. In contrast, models trained for image and text generation rely on a single token that acts as a narrow gate for the visual information. We demonstrate that ablating this single token significantly deteriorates performance on image understanding tasks. Furthermore, modifying this token enables effective steering of the image semantics, showing that targeted, local interventions can reliably control the model's global behavior.

Persistent Topological Features in Large Language Models

Understanding the decision-making processes of large language models (LLMs) is critical given their widespread applications. Towards this goal, describing the topological and geometrical properties of internal representations has recently provided valuable insights. For a more comprehensive characterization of these inherently complex spaces, we present a novel framework based on zigzag persistence, a method in topological data analysis (TDA) well-suited for describing data undergoing dynamic transformations across layers. Within this framework, we introduce persistence similarity, a new metric that quantifies the persistence and transformation of topological features such as $p$-cycles throughout the model layers. Unlike traditional similarity measures, our approach captures the entire evolutionary trajectory of these features, providing deeper insights into the internal workings of LLMs. As a practical application, we leverage persistence similarity to identify and prune redundant layers, demonstrating comparable performance to state-of-the-art methods across several benchmark datasets. Additionally, our analysis reveals consistent topological behaviors across various models and hyperparameter settings, suggesting a universal structure in LLM internal representations.

The representation landscape of few-shot learning and fine-tuning in large language models

In-context learning (ICL) and supervised fine-tuning (SFT) are two common strategies for improving the performance of modern large language models (LLMs) on specific tasks. Despite their different natures, these strategies often lead to comparable performance gains. However, little is known about whether they induce similar representations inside LLMs. We approach this problem by analyzing the probability landscape of their hidden representations in the two cases. More specifically, we compare how LLMs solve the same question-answering task, finding that ICL and SFT create very different internal structures, in both cases undergoing a sharp transition in the middle of the network. In the first half of the network, ICL shapes interpretable representations hierarchically organized according to their semantic content. In contrast, the probability landscape obtained with SFT is fuzzier and semantically mixed. In the second half of the model, the fine-tuned representations develop probability modes that better encode the identity of answers, while the landscape of ICL representations is characterized by less defined peaks. Our approach reveals the diverse computational strategies developed inside LLMs to solve the same task across different conditions, allowing us to make a step towards designing optimal methods to extract information from language models.

Detach-ROCKET: Sequential feature selection for time series classification with random convolutional kernels

Time series classification is essential in many fields, such as medicine, finance, environmental science, and manufacturing, enabling tasks like disease diagnosis, anomaly detection, and stock price prediction. Machine learning models like Recurrent Neural Networks and InceptionTime, while successful in numerous applications, can face scalability limitations due to intensive training requirements. To address this, random convolutional kernel models such as Rocket and its derivatives have emerged, simplifying training and achieving state-of-the-art performance by utilizing a large number of randomly generated features from time series data. However, due to their random nature, most of the generated features are redundant or non-informative, adding unnecessary computational load and compromising generalization. Here, we introduce Sequential Feature Detachment (SFD) as a method to identify and prune these non-essential features. SFD uses model coefficients to estimate feature importance and, unlike previous algorithms, can handle large feature sets without the need for complex hyperparameter tuning. Testing on the UCR archive demonstrates that SFD can produce models with $10\%$ of the original features while improving $0.2\%$ the accuracy on the test set. We also present an end-to-end procedure for determining an optimal balance between the number of features and model accuracy, called Detach-ROCKET. When applied to the largest binary UCR dataset, Detach-ROCKET is capable of reduce model size by $98.9\%$ and increases test accuracy by $0.6\%$.

Emergent representations in networks trained with the Forward-Forward algorithm

The Backpropagation algorithm, widely used to train neural networks, has often been criticised for its lack of biological realism. In an attempt to find a more biologically plausible alternative, and avoid to back-propagate gradients in favour of using local learning rules, the recently introduced Forward-Forward algorithm replaces the traditional forward and backward passes of Backpropagation with two forward passes. In this work, we show that internal representations obtained with the Forward-Forward algorithm organize into robust, category-specific ensembles, composed by an extremely low number of active units (high sparsity). This is remarkably similar to what is observed in cortical representations during sensory processing. While not found in models trained with standard Backpropagation, sparsity emerges also in networks optimized by Backpropagation, on the same training objective of Forward-Forward. These results suggest that the learning procedure proposed by Forward-Forward may be superior to Backpropagation in modelling learning in the cortex, even when a backward pass is used.

The geometry of hidden representations of large transformer models

Large transformers are powerful architectures for self-supervised analysis of data of various nature, ranging from protein sequences to text to images. In these models, the data representation in the hidden layers live in the same space, and the semantic structure of the dataset emerges by a sequence of functionally identical transformations between one representation and the next. We here characterize the geometric and statistical properties of these representations, focusing on the evolution of such proprieties across the layers. By analyzing geometric properties such as the intrinsic dimension (ID) and the neighbor composition we find that the representations evolve in a strikingly similar manner in transformers trained on protein language tasks and image reconstruction tasks. In the first layers, the data manifold expands, becoming high-dimensional, and then it contracts significantly in the intermediate layers. In the last part of the model, the ID remains approximately constant or forms a second shallow peak. We show that the semantic complexity of the dataset emerges at the end of the first peak. This phenomenon can be observed across many models trained on diverse datasets. Based on these observations, we suggest using the ID profile as an unsupervised proxy to identify the layers which are more suitable for downstream learning tasks.

Hierarchical nucleation in deep neural networks

Deep convolutional networks (DCNs) learn meaningful representations where data that share the same abstract characteristics are positioned closer and closer. Understanding these representations and how they are generated is of unquestioned practical and theoretical interest. In this work we study the evolution of the probability density of the ImageNet dataset across the hidden layers in some state-of-the-art DCNs. We find that the initial layers generate a unimodal probability density getting rid of any structure irrelevant for classification. In subsequent layers density peaks arise in a hierarchical fashion that mirrors the semantic hierarchy of the concepts. Density peaks corresponding to single categories appear only close to the output and via a very sharp transition which resembles the nucleation process of a heterogeneous liquid. This process leaves a footprint in the probability density of the output layer where the topography of the peaks allows reconstructing the semantic relationships of the categories.

Intrinsic dimension of data representations in deep neural networks

Deep neural networks progressively transform their inputs across multiple processing layers. What are the geometrical properties of the representations learned by these networks? Here we study the intrinsic dimensionality (ID) of data-representations, i.e. the minimal number of parameters needed to describe a representation. We find that, in a trained network, the ID is orders of magnitude smaller than the number of units in each layer. Across layers, the ID first increases and then progressively decreases in the final layers. Remarkably, the ID of the last hidden layer predicts classification accuracy on the test set. These results can neither be found by linear dimensionality estimates (e.g., with principal component analysis), nor in representations that had been artificially linearized. They are neither found in untrained networks, nor in networks that are trained on randomized labels. This suggests that neural networks that can generalize are those that transform the data into low-dimensional, but not necessarily flat manifolds.