The Geometry of Tokens in Internal Representations of Large Language Models

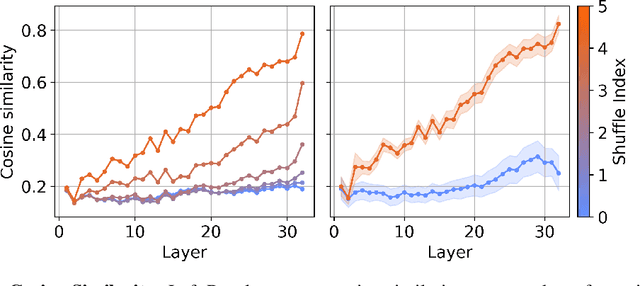
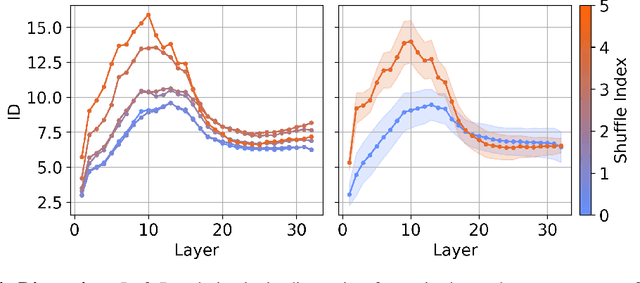
We investigate the relationship between the geometry of token embeddings and their role in the next token prediction within transformer models. An important aspect of this connection uses the notion of empirical measure, which encodes the distribution of token point clouds across transformer layers and drives the evolution of token representations in the mean-field interacting picture. We use metrics such as intrinsic dimension, neighborhood overlap, and cosine similarity to observationally probe these empirical measures across layers. To validate our approach, we compare these metrics to a dataset where the tokens are shuffled, which disrupts the syntactic and semantic structure. Our findings reveal a correlation between the geometric properties of token embeddings and the cross-entropy loss of next token predictions, implying that prompts with higher loss values have tokens represented in higher-dimensional spaces.

Persistent Topological Features in Large Language Models

Understanding the decision-making processes of large language models (LLMs) is critical given their widespread applications. Towards this goal, describing the topological and geometrical properties of internal representations has recently provided valuable insights. For a more comprehensive characterization of these inherently complex spaces, we present a novel framework based on zigzag persistence, a method in topological data analysis (TDA) well-suited for describing data undergoing dynamic transformations across layers. Within this framework, we introduce persistence similarity, a new metric that quantifies the persistence and transformation of topological features such as $p$-cycles throughout the model layers. Unlike traditional similarity measures, our approach captures the entire evolutionary trajectory of these features, providing deeper insights into the internal workings of LLMs. As a practical application, we leverage persistence similarity to identify and prune redundant layers, demonstrating comparable performance to state-of-the-art methods across several benchmark datasets. Additionally, our analysis reveals consistent topological behaviors across various models and hyperparameter settings, suggesting a universal structure in LLM internal representations.

Topological Echoes of Primordial Physics in the Universe at Large Scales

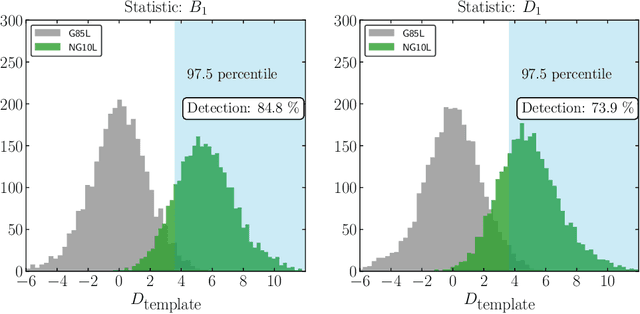
We present a pipeline for characterizing and constraining initial conditions in cosmology via persistent homology. The cosmological observable of interest is the cosmic web of large scale structure, and the initial conditions in question are non-Gaussianities (NG) of primordial density perturbations. We compute persistence diagrams and derived statistics for simulations of dark matter halos with Gaussian and non-Gaussian initial conditions. For computational reasons and to make contact with experimental observations, our pipeline computes persistence in sub-boxes of full simulations and simulations are subsampled to uniform halo number. We use simulations with large NG ($f_{\rm NL}^{\rm loc}=250$) as templates for identifying data with mild NG ($f_{\rm NL}^{\rm loc}=10$), and running the pipeline on several cubic volumes of size $40~(\textrm{Gpc/h})^{3}$, we detect $f_{\rm NL}^{\rm loc}=10$ at $97.5\%$ confidence on $\sim 85\%$ of the volumes for our best single statistic. Throughout we benefit from the interpretability of topological features as input for statistical inference, which allows us to make contact with previous first-principles calculations and make new predictions.