Learning to Trace Seiberg Dualities

Dualities play an important role in establishing both microscopic and emergent phenomena in a wide range of physical systems. In practice, though, it can often be computationally challenging to establish when two systems are dual, even when all of the "rules of the game" are well-known. Said differently, when confronted with two systems, how can one efficiently establish that they are in fact dual? In this paper we use machine learning methods to address this question for Seiberg dualities of supersymmetric quiver gauge theories. Mathematically, this involves establishing mutations of quivers, which is in turn a variation on the theme of "learning to unknot". On the one hand, this leads us to a practical tool for establishing the computational complexity of different dualities. On the other hand, it also allows us to study how different network architectures learn how to trace Seiberg dualities. We find that for quivers with a modest number of quiver nodes (of order $10$), different network architectures consisting of transformers and multi-layer perceptrons tend to outperform deterministic algorithms. Supplementing the network by well-established pathfinder algorithms (essentially "Google Maps for quivers") leads to an additional improvement in the efficiency and accuracy of the search strategy. We anticipate that this class of questions can serve as a useful benchmark for frontier AI models applied to theoretical physics.

Generating Special Triangulations with Transformers

Triangulations, i.e., well-structured decompositions of geometric objects into triangle-like pieces, are central objects in many domains of mathematics and physics. In particular, fine, regular, and star triangulations (FRSTs) of 4D reflexive polytopes give rise to smooth Calabi-Yau threefolds, which are of significant interest in string theory. However, the high dimensionality and combinatorial complexity of triangulations make them particularly challenging to model with classical numerical methods or machine learning. In this work, we show that transformers, equipped with an appropriate encoding scheme, can be effectively trained to representatively generate new FRSTs across a range of polytope sizes. Moreover, these models can also self-improve through retraining on their own output. This opens the door to both concrete applications to the classification of Calabi-Yau manifolds and further research in physics, combinatorics and algebraic geometry.

Cosmology with Persistent Homology: Parameter Inference via Machine Learning

Building upon [2308.02636], this article investigates the potential constraining power of persistent homology for cosmological parameters and primordial non-Gaussianity amplitudes in a likelihood-free inference pipeline. We evaluate the ability of persistence images (PIs) to infer parameters, compared to the combined Power Spectrum and Bispectrum (PS/BS), and we compare two types of models: neural-based, and tree-based. PIs consistently lead to better predictions compared to the combined PS/BS when the parameters can be constrained (i.e., for $\{\Omega_{\rm m}, \sigma_8, n_{\rm s}, f_{\rm NL}^{\rm loc}\}$). PIs perform particularly well for $f_{\rm NL}^{\rm loc}$, showing the promise of persistent homology in constraining primordial non-Gaussianity. Our results show that combining PIs with PS/BS provides only marginal gains, indicating that the PS/BS contains little extra or complementary information to the PIs. Finally, we provide a visualization of the most important topological features for $f_{\rm NL}^{\rm loc}$ and for $\Omega_{\rm m}$. This reveals that clusters and voids (0-cycles and 2-cycles) are most informative for $\Omega_{\rm m}$, while $f_{\rm NL}^{\rm loc}$ uses the filaments (1-cycles) in addition to the other two types of topological features.

Learning from Topology: Cosmological Parameter Estimation from the Large-scale Structure

The topology of the large-scale structure of the universe contains valuable information on the underlying cosmological parameters. While persistent homology can extract this topological information, the optimal method for parameter estimation from the tool remains an open question. To address this, we propose a neural network model to map persistence images to cosmological parameters. Through a parameter recovery test, we demonstrate that our model makes accurate and precise estimates, considerably outperforming conventional Bayesian inference approaches.

Breeding realistic D-brane models

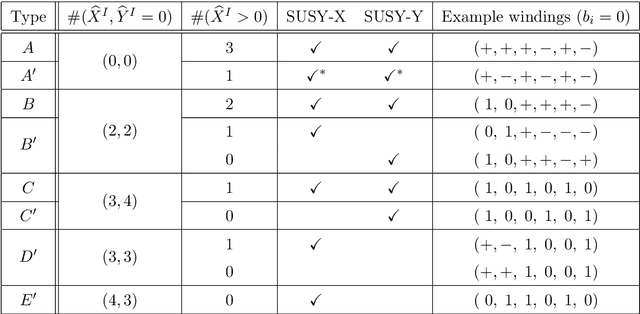
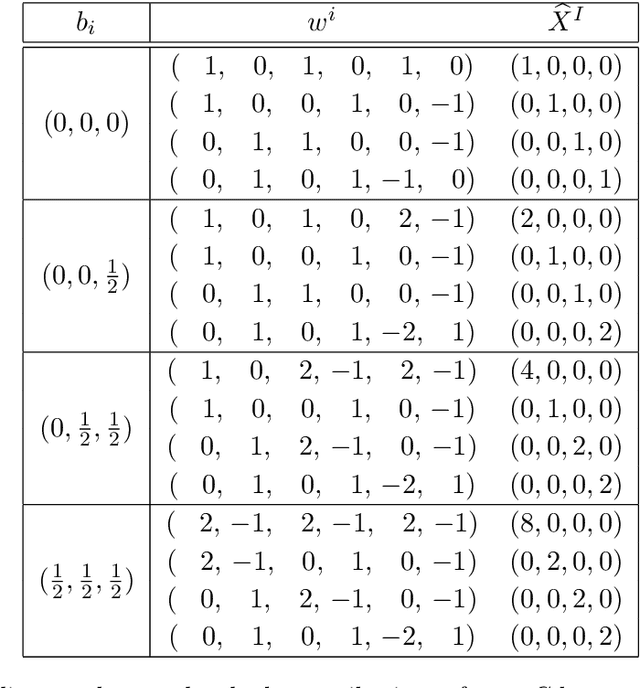
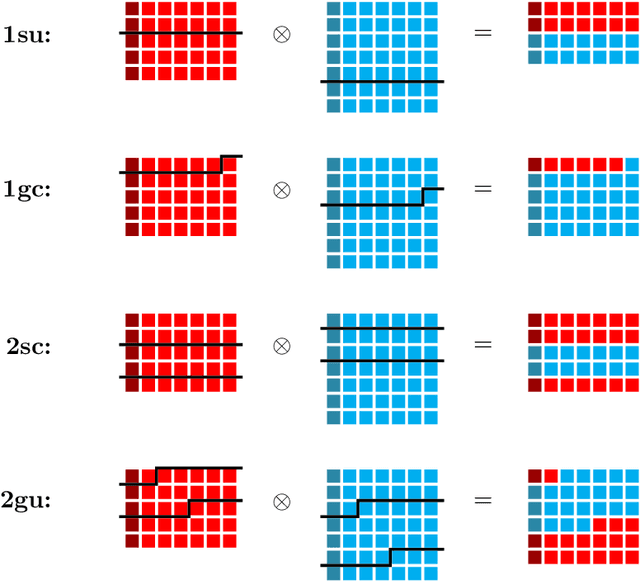
Intersecting branes provide a useful mechanism to construct particle physics models from string theory with a wide variety of desirable characteristics. The landscape of such models can be enormous, and navigating towards regions which are most phenomenologically interesting is potentially challenging. Machine learning techniques can be used to efficiently construct large numbers of consistent and phenomenologically desirable models. In this work we phrase the problem of finding consistent intersecting D-brane models in terms of genetic algorithms, which mimic natural selection to evolve a population collectively towards optimal solutions. For a four-dimensional ${\cal N}=1$ supersymmetric type IIA orientifold with intersecting D6-branes, we demonstrate that $\mathcal{O}(10^6)$ unique, fully consistent models can be easily constructed, and, by a judicious choice of search environment and hyper-parameters, $\mathcal{O}(30\%)$ of the found models contain the desired Standard Model gauge group factor. Having a sizable sample allows us to draw some preliminary landscape statistics of intersecting brane models both with and without the restriction of having the Standard Model gauge factor.

Topological Echoes of Primordial Physics in the Universe at Large Scales

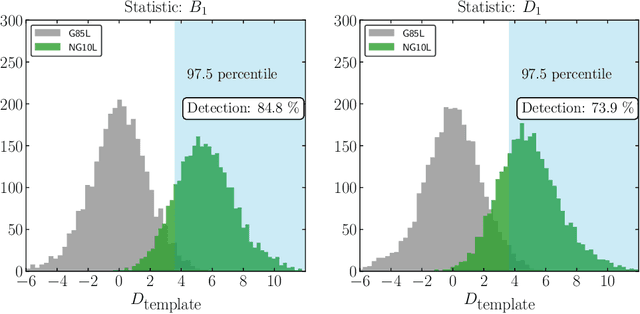
We present a pipeline for characterizing and constraining initial conditions in cosmology via persistent homology. The cosmological observable of interest is the cosmic web of large scale structure, and the initial conditions in question are non-Gaussianities (NG) of primordial density perturbations. We compute persistence diagrams and derived statistics for simulations of dark matter halos with Gaussian and non-Gaussian initial conditions. For computational reasons and to make contact with experimental observations, our pipeline computes persistence in sub-boxes of full simulations and simulations are subsampled to uniform halo number. We use simulations with large NG ($f_{\rm NL}^{\rm loc}=250$) as templates for identifying data with mild NG ($f_{\rm NL}^{\rm loc}=10$), and running the pipeline on several cubic volumes of size $40~(\textrm{Gpc/h})^{3}$, we detect $f_{\rm NL}^{\rm loc}=10$ at $97.5\%$ confidence on $\sim 85\%$ of the volumes for our best single statistic. Throughout we benefit from the interpretability of topological features as input for statistical inference, which allows us to make contact with previous first-principles calculations and make new predictions.

Interpretable Phase Detection and Classification with Persistent Homology

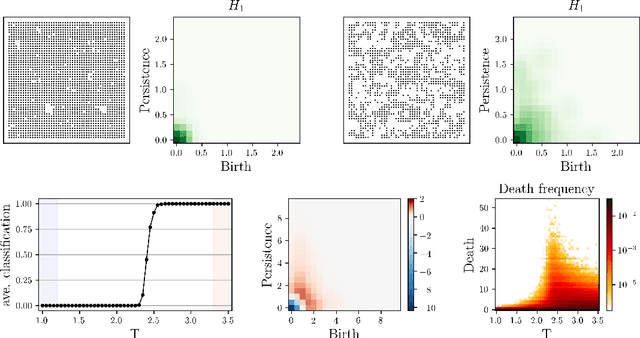
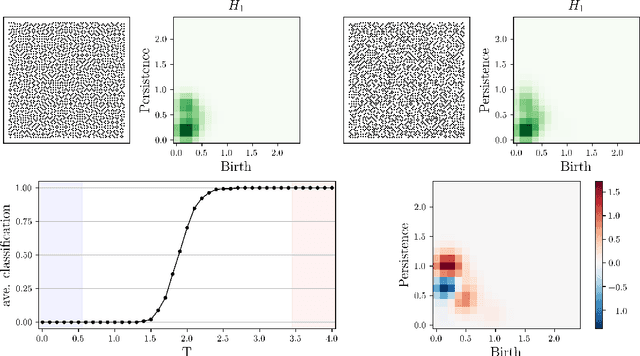
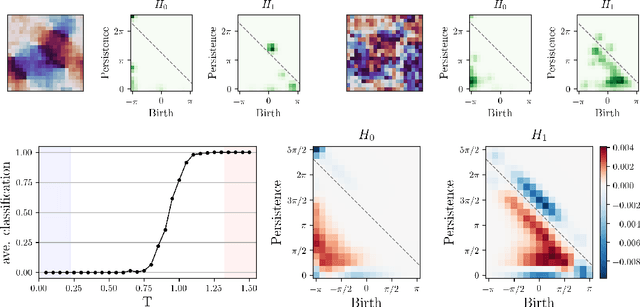
We apply persistent homology to the task of discovering and characterizing phase transitions, using lattice spin models from statistical physics for working examples. Persistence images provide a useful representation of the homological data for conducting statistical tasks. To identify the phase transitions, a simple logistic regression on these images is sufficient for the models we consider, and interpretable order parameters are then read from the weights of the regression. Magnetization, frustration and vortex-antivortex structure are identified as relevant features for characterizing phase transitions.

Searching the Landscape of Flux Vacua with Genetic Algorithms

In this paper, we employ genetic algorithms to explore the landscape of type IIB flux vacua. We show that genetic algorithms can efficiently scan the landscape for viable solutions satisfying various criteria. More specifically, we consider a symmetric $T^{6}$ as well as the conifold region of a Calabi-Yau hypersurface. We argue that in both cases genetic algorithms are powerful tools for finding flux vacua with interesting phenomenological properties. We also compare genetic algorithms to algorithms based on different breeding mechanisms as well as random walk approaches.