Breeding realistic D-brane models

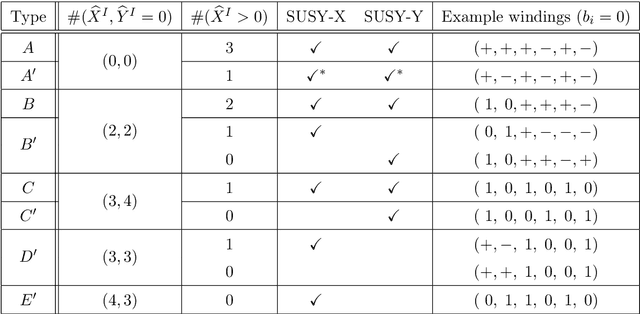
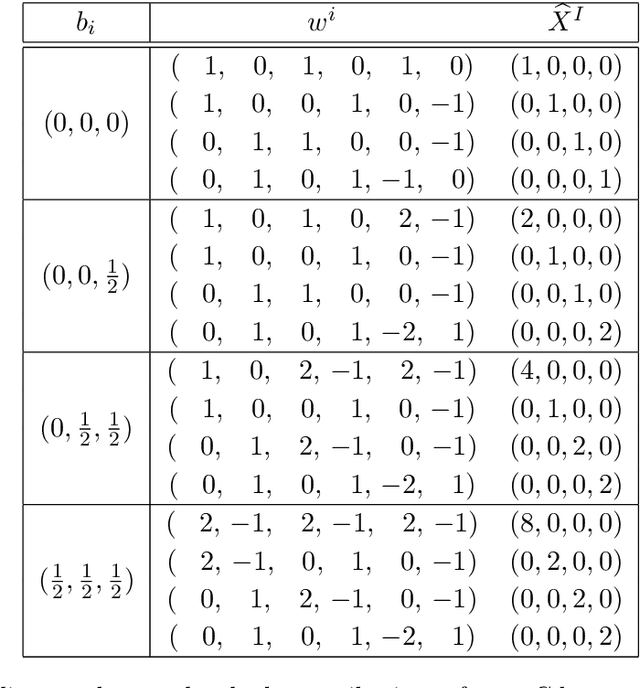
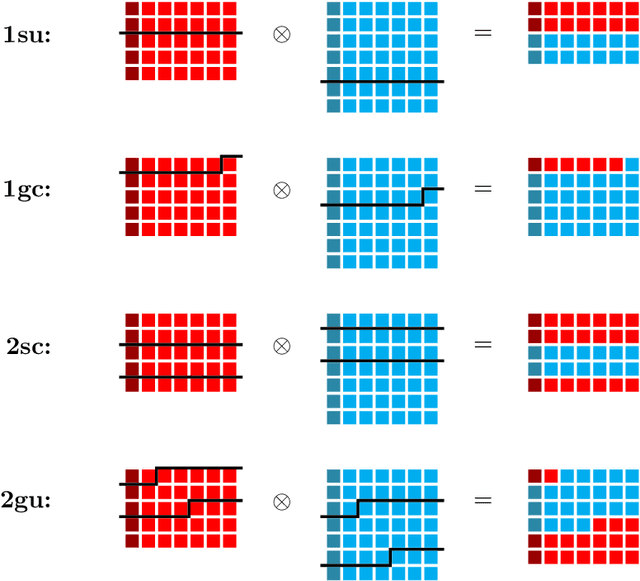
Intersecting branes provide a useful mechanism to construct particle physics models from string theory with a wide variety of desirable characteristics. The landscape of such models can be enormous, and navigating towards regions which are most phenomenologically interesting is potentially challenging. Machine learning techniques can be used to efficiently construct large numbers of consistent and phenomenologically desirable models. In this work we phrase the problem of finding consistent intersecting D-brane models in terms of genetic algorithms, which mimic natural selection to evolve a population collectively towards optimal solutions. For a four-dimensional ${\cal N}=1$ supersymmetric type IIA orientifold with intersecting D6-branes, we demonstrate that $\mathcal{O}(10^6)$ unique, fully consistent models can be easily constructed, and, by a judicious choice of search environment and hyper-parameters, $\mathcal{O}(30\%)$ of the found models contain the desired Standard Model gauge group factor. Having a sizable sample allows us to draw some preliminary landscape statistics of intersecting brane models both with and without the restriction of having the Standard Model gauge factor.

Interpretable Phase Detection and Classification with Persistent Homology

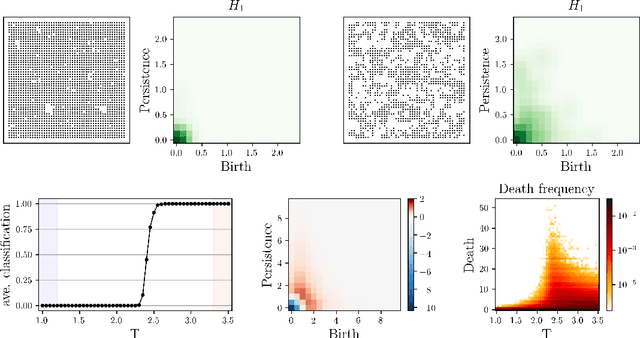
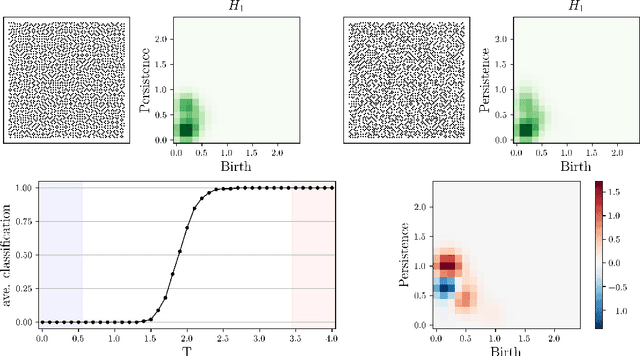
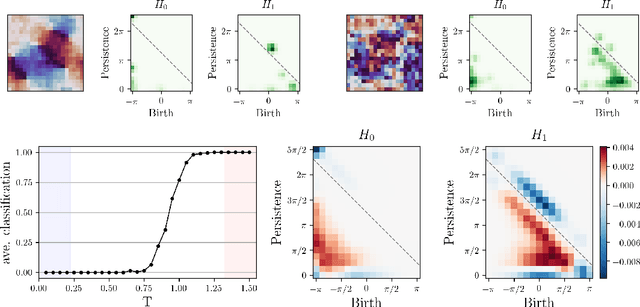
We apply persistent homology to the task of discovering and characterizing phase transitions, using lattice spin models from statistical physics for working examples. Persistence images provide a useful representation of the homological data for conducting statistical tasks. To identify the phase transitions, a simple logistic regression on these images is sufficient for the models we consider, and interpretable order parameters are then read from the weights of the regression. Magnetization, frustration and vortex-antivortex structure are identified as relevant features for characterizing phase transitions.