Interpretable Phase Detection and Classification with Persistent Homology
Paper and Code
Dec 01, 2020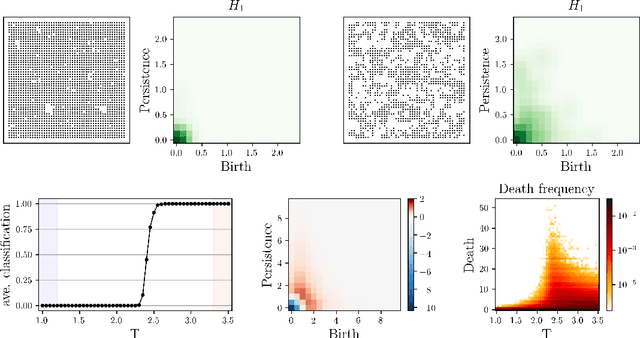
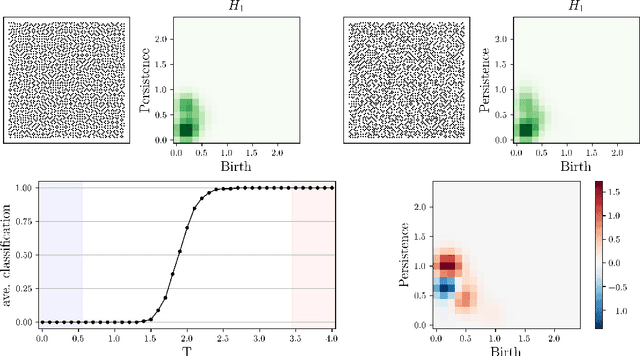
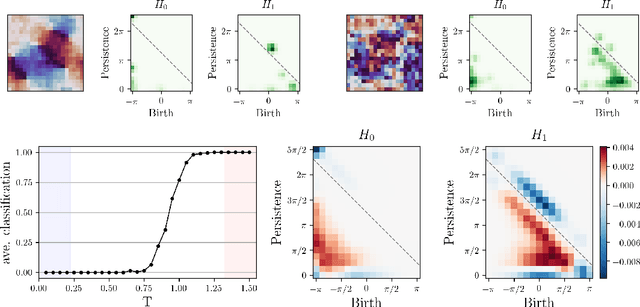
We apply persistent homology to the task of discovering and characterizing phase transitions, using lattice spin models from statistical physics for working examples. Persistence images provide a useful representation of the homological data for conducting statistical tasks. To identify the phase transitions, a simple logistic regression on these images is sufficient for the models we consider, and interpretable order parameters are then read from the weights of the regression. Magnetization, frustration and vortex-antivortex structure are identified as relevant features for characterizing phase transitions.
* 5 pages, 3 figures; shortened version of arXiv:2009.14231; accepted
to NeurIPS 2020 Workshop on Topological Data Analysis and Beyond
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge