Prune and distill: similar reformatting of image information along rat visual cortex and deep neural networks

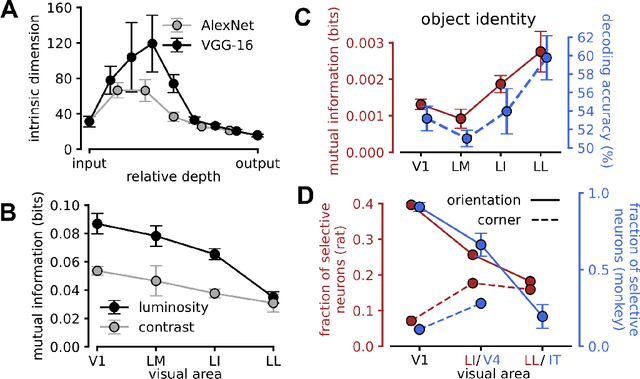
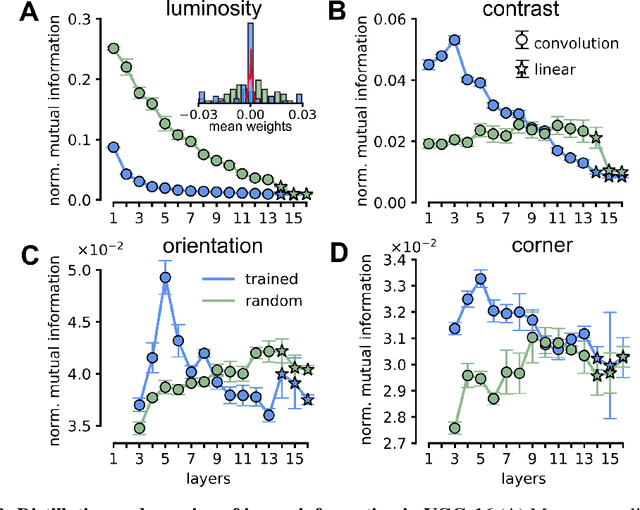
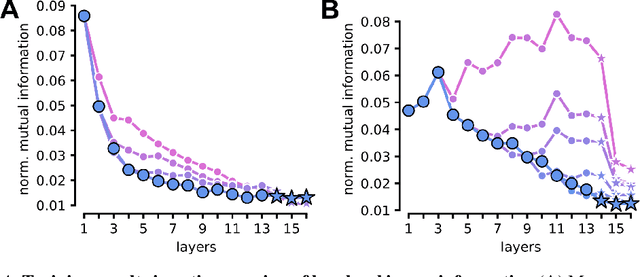
Visual object recognition has been extensively studied in both neuroscience and computer vision. Recently, the most popular class of artificial systems for this task, deep convolutional neural networks (CNNs), has been shown to provide excellent models for its functional analogue in the brain, the ventral stream in visual cortex. This has prompted questions on what, if any, are the common principles underlying the reformatting of visual information as it flows through a CNN or the ventral stream. Here we consider some prominent statistical patterns that are known to exist in the internal representations of either CNNs or the visual cortex and look for them in the other system. We show that intrinsic dimensionality (ID) of object representations along the rat homologue of the ventral stream presents two distinct expansion-contraction phases, as previously shown for CNNs. Conversely, in CNNs, we show that training results in both distillation and active pruning (mirroring the increase in ID) of low- to middle-level image information in single units, as representations gain the ability to support invariant discrimination, in agreement with previous observations in rat visual cortex. Taken together, our findings suggest that CNNs and visual cortex share a similarly tight relationship between dimensionality expansion/reduction of object representations and reformatting of image information.

Intrinsic dimension of data representations in deep neural networks

Deep neural networks progressively transform their inputs across multiple processing layers. What are the geometrical properties of the representations learned by these networks? Here we study the intrinsic dimensionality (ID) of data-representations, i.e. the minimal number of parameters needed to describe a representation. We find that, in a trained network, the ID is orders of magnitude smaller than the number of units in each layer. Across layers, the ID first increases and then progressively decreases in the final layers. Remarkably, the ID of the last hidden layer predicts classification accuracy on the test set. These results can neither be found by linear dimensionality estimates (e.g., with principal component analysis), nor in representations that had been artificially linearized. They are neither found in untrained networks, nor in networks that are trained on randomized labels. This suggests that neural networks that can generalize are those that transform the data into low-dimensional, but not necessarily flat manifolds.

Characterization of Visual Object Representations in Rat Primary Visual Cortex

For most animal species, quick and reliable identification of visual objects is critical for survival. This applies also to rodents, which, in recent years, have become increasingly popular models of visual functions. For this reason in this work we analyzed how various properties of visual objects are represented in rat primary visual cortex (V1). The analysis has been carried out through supervised (classification) and unsupervised (clustering) learning methods. We assessed quantitatively the discrimination capabilities of V1 neurons by demonstrating how photometric properties (luminosity and object position in the scene) can be derived directly from the neuronal responses.