ResiDual Transformer Alignment with Spectral Decomposition

When examined through the lens of their residual streams, a puzzling property emerges in transformer networks: residual contributions (e.g., attention heads) sometimes specialize in specific tasks or input attributes. In this paper, we analyze this phenomenon in vision transformers, focusing on the spectral geometry of residuals, and explore its implications for modality alignment in vision-language models. First, we link it to the intrinsically low-dimensional structure of visual head representations, zooming into their principal components and showing that they encode specialized roles across a wide variety of input data distributions. Then, we analyze the effect of head specialization in multimodal models, focusing on how improved alignment between text and specialized heads impacts zero-shot classification performance. This specialization-performance link consistently holds across diverse pre-training data, network sizes, and objectives, demonstrating a powerful new mechanism for boosting zero-shot classification through targeted alignment. Ultimately, we translate these insights into actionable terms by introducing ResiDual, a technique for spectral alignment of the residual stream. Much like panning for gold, it lets the noise from irrelevant unit principal components (i.e., attributes) wash away to amplify task-relevant ones. Remarkably, this dual perspective on modality alignment yields fine-tuning level performances on different data distributions while modeling an extremely interpretable and parameter-efficient transformation, as we extensively show on more than 50 (pre-trained network, dataset) pairs.

Latent Functional Maps

Neural models learn data representations that lie on low-dimensional manifolds, yet modeling the relation between these representational spaces is an ongoing challenge. By integrating spectral geometry principles into neural modeling, we show that this problem can be better addressed in the functional domain, mitigating complexity, while enhancing interpretability and performances on downstream tasks. To this end, we introduce a multi-purpose framework to the representation learning community, which allows to: (i) compare different spaces in an interpretable way and measure their intrinsic similarity; (ii) find correspondences between them, both in unsupervised and weakly supervised settings, and (iii) to effectively transfer representations between distinct spaces. We validate our framework on various applications, ranging from stitching to retrieval tasks, demonstrating that latent functional maps can serve as a swiss-army knife for representation alignment.

Latent Space Translation via Inverse Relative Projection

The emergence of similar representations between independently trained neural models has sparked significant interest in the representation learning community, leading to the development of various methods to obtain communication between latent spaces. "Latent space communication" can be achieved in two ways: i) by independently mapping the original spaces to a shared or relative one; ii) by directly estimating a transformation from a source latent space to a target one. In this work, we combine the two into a novel method to obtain latent space translation through the relative space. By formalizing the invertibility of angle-preserving relative representations and assuming the scale invariance of decoder modules in neural models, we can effectively use the relative space as an intermediary, independently projecting onto and from other semantically similar spaces. Extensive experiments over various architectures and datasets validate our scale invariance assumption and demonstrate the high accuracy of our method in latent space translation. We also apply our method to zero-shot stitching between arbitrary pre-trained text and image encoders and their classifiers, even across modalities. Our method has significant potential for facilitating the reuse of models in a practical manner via compositionality.

Latent. Functional Map

Neural models learn data representations that lie on low-dimensional manifolds, yet modeling the relation between these representational spaces is an ongoing challenge. By integrating spectral geometry principles into neural modeling, we show that this problem can be better addressed in the functional domain, mitigating complexity, while enhancing interpretability and performances on downstream tasks. To this end, we introduce a multi-purpose framework to the representation learning community, which allows to: (i) compare different spaces in an interpretable way and measure their intrinsic similarity; (ii) find correspondences between them, both in unsupervised and weakly supervised settings, and (iii) to effectively transfer representations between distinct spaces. We validate our framework on various applications, ranging from stitching to retrieval tasks, demonstrating that latent functional maps can serve as a swiss-army knife for representation alignment.

Scalable unsupervised alignment of general metric and non-metric structures

Aligning data from different domains is a fundamental problem in machine learning with broad applications across very different areas, most notably aligning experimental readouts in single-cell multiomics. Mathematically, this problem can be formulated as the minimization of disagreement of pair-wise quantities such as distances and is related to the Gromov-Hausdorff and Gromov-Wasserstein distances. Computationally, it is a quadratic assignment problem (QAP) that is known to be NP-hard. Prior works attempted to solve the QAP directly with entropic or low-rank regularization on the permutation, which is computationally tractable only for modestly-sized inputs, and encode only limited inductive bias related to the domains being aligned. We consider the alignment of metric structures formulated as a discrete Gromov-Wasserstein problem and instead of solving the QAP directly, we propose to learn a related well-scalable linear assignment problem (LAP) whose solution is also a minimizer of the QAP. We also show a flexible extension of the proposed framework to general non-metric dissimilarities through differentiable ranks. We extensively evaluate our approach on synthetic and real datasets from single-cell multiomics and neural latent spaces, achieving state-of-the-art performance while being conceptually and computationally simple.

Zero-Shot Stitching in Reinforcement Learning using Relative Representations

Visual Reinforcement Learning is a popular and powerful framework that takes full advantage of the Deep Learning breakthrough. However, it is also known that variations in the input (e.g., different colors of the panorama due to the season of the year) or the task (e.g., changing the speed limit for a car to respect) could require complete retraining of the agents. In this work, we leverage recent developments in unifying latent representations to demonstrate that it is possible to combine the components of an agent, rather than retrain it from scratch. We build upon the recent relative representations framework and adapt it for Visual RL. This allows us to create completely new agents capable of handling environment-task combinations never seen during training. Our work paves the road toward a more accessible and flexible use of reinforcement learning.

Latent Space Translation via Semantic Alignment

While different neural models often exhibit latent spaces that are alike when exposed to semantically related data, this intrinsic similarity is not always immediately discernible. Towards a better understanding of this phenomenon, our work shows how representations learned from these neural modules can be translated between different pre-trained networks via simpler transformations than previously thought. An advantage of this approach is the ability to estimate these transformations using standard, well-understood algebraic procedures that have closed-form solutions. Our method directly estimates a transformation between two given latent spaces, thereby enabling effective stitching of encoders and decoders without additional training. We extensively validate the adaptability of this translation procedure in different experimental settings: across various trainings, domains, architectures (e.g., ResNet, CNN, ViT), and in multiple downstream tasks (classification, reconstruction). Notably, we show how it is possible to zero-shot stitch text encoders and vision decoders, or vice-versa, yielding surprisingly good classification performance in this multimodal setting.

From Bricks to Bridges: Product of Invariances to Enhance Latent Space Communication

It has been observed that representations learned by distinct neural networks conceal structural similarities when the models are trained under similar inductive biases. From a geometric perspective, identifying the classes of transformations and the related invariances that connect these representations is fundamental to unlocking applications, such as merging, stitching, and reusing different neural modules. However, estimating task-specific transformations a priori can be challenging and expensive due to several factors (e.g., weights initialization, training hyperparameters, or data modality). To this end, we introduce a versatile method to directly incorporate a set of invariances into the representations, constructing a product space of invariant components on top of the latent representations without requiring prior knowledge about the optimal invariance to infuse. We validate our solution on classification and reconstruction tasks, observing consistent latent similarity and downstream performance improvements in a zero-shot stitching setting. The experimental analysis comprises three modalities (vision, text, and graphs), twelve pretrained foundational models, eight benchmarks, and several architectures trained from scratch.

Accelerating Transformer Inference for Translation via Parallel Decoding

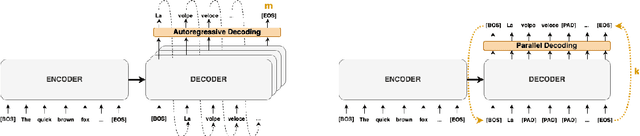
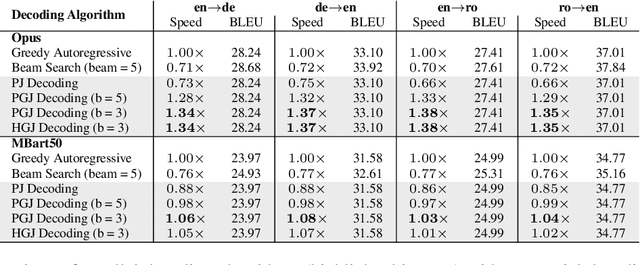
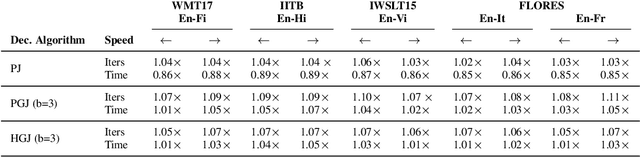
Autoregressive decoding limits the efficiency of transformers for Machine Translation (MT). The community proposed specific network architectures and learning-based methods to solve this issue, which are expensive and require changes to the MT model, trading inference speed at the cost of the translation quality. In this paper, we propose to address the problem from the point of view of decoding algorithms, as a less explored but rather compelling direction. We propose to reframe the standard greedy autoregressive decoding of MT with a parallel formulation leveraging Jacobi and Gauss-Seidel fixed-point iteration methods for fast inference. This formulation allows to speed up existing models without training or modifications while retaining translation quality. We present three parallel decoding algorithms and test them on different languages and models showing how the parallelization introduces a speedup up to 38% w.r.t. the standard autoregressive decoding and nearly 2x when scaling the method on parallel resources. Finally, we introduce a decoding dependency graph visualizer (DDGviz) that let us see how the model has learned the conditional dependence between tokens and inspect the decoding procedure.

Attention-likelihood relationship in transformers

We analyze how large language models (LLMs) represent out-of-context words, investigating their reliance on the given context to capture their semantics. Our likelihood-guided text perturbations reveal a correlation between token likelihood and attention values in transformer-based language models. Extensive experiments reveal that unexpected tokens cause the model to attend less to the information coming from themselves to compute their representations, particularly at higher layers. These findings have valuable implications for assessing the robustness of LLMs in real-world scenarios. Fully reproducible codebase at https://github.com/Flegyas/AttentionLikelihood.