Representing local protein environments with atomistic foundation models

The local structure of a protein strongly impacts its function and interactions with other molecules. Therefore, a concise, informative representation of a local protein environment is essential for modeling and designing proteins and biomolecular interactions. However, these environments' extensive structural and chemical variability makes them challenging to model, and such representations remain under-explored. In this work, we propose a novel representation for a local protein environment derived from the intermediate features of atomistic foundation models (AFMs). We demonstrate that this embedding effectively captures both local structure (e.g., secondary motifs), and chemical features (e.g., amino-acid identity and protonation state). We further show that the AFM-derived representation space exhibits meaningful structure, enabling the construction of data-driven priors over the distribution of biomolecular environments. Finally, in the context of biomolecular NMR spectroscopy, we demonstrate that the proposed representations enable a first-of-its-kind physics-informed chemical shift predictor that achieves state-of-the-art accuracy. Our results demonstrate the surprising effectiveness of atomistic foundation models and their emergent representations for protein modeling beyond traditional molecular simulations. We believe this will open new lines of work in constructing effective functional representations for protein environments.

From Lab to Wrist: Bridging Metabolic Monitoring and Consumer Wearables for Heart Rate and Oxygen Consumption Modeling

Understanding physiological responses during running is critical for performance optimization, tailored training prescriptions, and athlete health management. We introduce a comprehensive framework -- what we believe to be the first capable of predicting instantaneous oxygen consumption (VO$_{2}$) trajectories exclusively from consumer-grade wearable data. Our approach employs two complementary physiological models: (1) accurate modeling of heart rate (HR) dynamics via a physiologically constrained ordinary differential equation (ODE) and neural Kalman filter, trained on over 3 million HR observations, achieving 1-second interval predictions with mean absolute errors as low as 2.81\,bpm (correlation 0.87); and (2) leveraging the principles of precise HR modeling, a novel VO$_{2}$ prediction architecture requiring only the initial second of VO$_{2}$ data for calibration, enabling robust, sequence-to-sequence metabolic demand estimation. Despite relying solely on smartwatch and chest-strap data, our method achieves mean absolute percentage errors of approximately 13\%, effectively capturing rapid physiological transitions and steady-state conditions across diverse running intensities. Our synchronized dataset, complemented by blood lactate measurements, further lays the foundation for future noninvasive metabolic zone identification. By embedding physiological constraints within modern machine learning, this framework democratizes advanced metabolic monitoring, bridging laboratory-grade accuracy and everyday accessibility, thus empowering both elite athletes and recreational fitness enthusiasts.

Generative modeling of protein ensembles guided by crystallographic electron densities

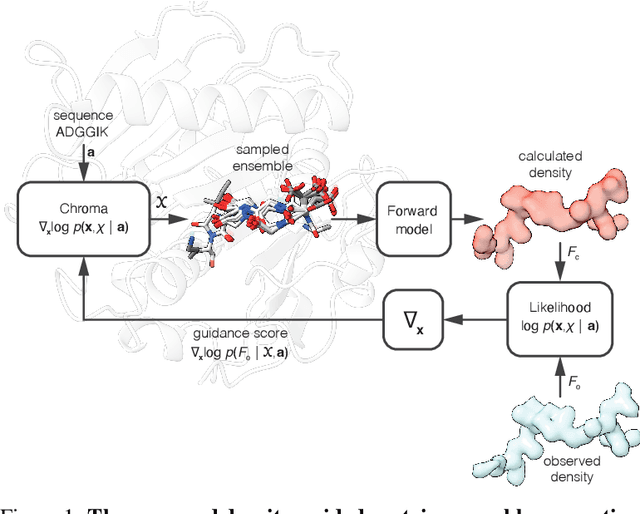
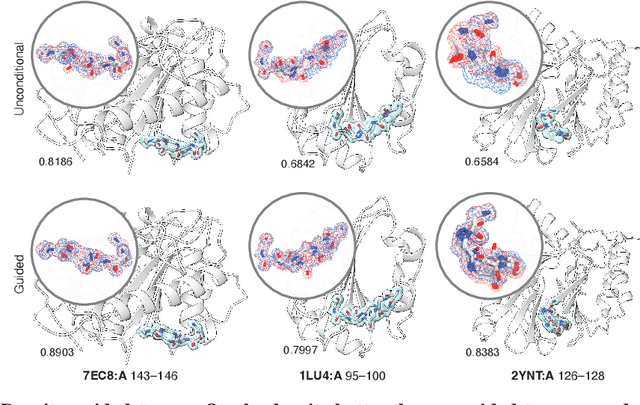
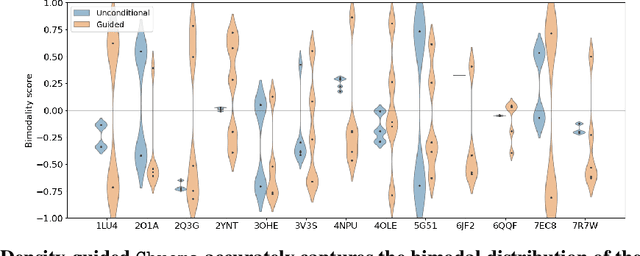
Proteins are dynamic, adopting ensembles of conformations. The nature of this conformational heterogenity is imprinted in the raw electron density measurements obtained from X-ray crystallography experiments. Fitting an ensemble of protein structures to these measurements is a challenging, ill-posed inverse problem. We propose a non-i.i.d. ensemble guidance approach to solve this problem using existing protein structure generative models and demonstrate that it accurately recovers complicated multi-modal alternate protein backbone conformations observed in certain single crystal measurements.

Scalable unsupervised alignment of general metric and non-metric structures

Aligning data from different domains is a fundamental problem in machine learning with broad applications across very different areas, most notably aligning experimental readouts in single-cell multiomics. Mathematically, this problem can be formulated as the minimization of disagreement of pair-wise quantities such as distances and is related to the Gromov-Hausdorff and Gromov-Wasserstein distances. Computationally, it is a quadratic assignment problem (QAP) that is known to be NP-hard. Prior works attempted to solve the QAP directly with entropic or low-rank regularization on the permutation, which is computationally tractable only for modestly-sized inputs, and encode only limited inductive bias related to the domains being aligned. We consider the alignment of metric structures formulated as a discrete Gromov-Wasserstein problem and instead of solving the QAP directly, we propose to learn a related well-scalable linear assignment problem (LAP) whose solution is also a minimizer of the QAP. We also show a flexible extension of the proposed framework to general non-metric dissimilarities through differentiable ranks. We extensively evaluate our approach on synthetic and real datasets from single-cell multiomics and neural latent spaces, achieving state-of-the-art performance while being conceptually and computationally simple.

Vector Quantile Regression on Manifolds

Quantile regression (QR) is a statistical tool for distribution-free estimation of conditional quantiles of a target variable given explanatory features. QR is limited by the assumption that the target distribution is univariate and defined on an Euclidean domain. Although the notion of quantiles was recently extended to multi-variate distributions, QR for multi-variate distributions on manifolds remains underexplored, even though many important applications inherently involve data distributed on, e.g., spheres (climate measurements), tori (dihedral angles in proteins), or Lie groups (attitude in navigation). By leveraging optimal transport theory and the notion of $c$-concave functions, we meaningfully define conditional vector quantile functions of high-dimensional variables on manifolds (M-CVQFs). Our approach allows for quantile estimation, regression, and computation of conditional confidence sets. We demonstrate the approach's efficacy and provide insights regarding the meaning of non-Euclidean quantiles through preliminary synthetic data experiments.

Fast Nonlinear Vector Quantile Regression

Quantile regression (QR) is a powerful tool for estimating one or more conditional quantiles of a target variable $\mathrm{Y}$ given explanatory features $\boldsymbol{\mathrm{X}}$. A limitation of QR is that it is only defined for scalar target variables, due to the formulation of its objective function, and since the notion of quantiles has no standard definition for multivariate distributions. Recently, vector quantile regression (VQR) was proposed as an extension of QR for high-dimensional target variables, thanks to a meaningful generalization of the notion of quantiles to multivariate distributions. Despite its elegance, VQR is arguably not applicable in practice due to several limitations: (i) it assumes a linear model for the quantiles of the target $\mathrm{Y}$ given the features $\boldsymbol{\mathrm{X}}$; (ii) its exact formulation is intractable even for modestly-sized problems in terms of target dimensions, number of regressed quantile levels, or number of features, and its relaxed dual formulation may violate the monotonicity of the estimated quantiles; (iii) no fast or scalable solvers for VQR currently exist. In this work we fully address these limitations, namely: (i) We extend VQR to the non-linear case, showing substantial improvement over linear VQR; (ii) We propose vector monotone rearrangement, a method which ensures the estimates obtained by VQR relaxations are monotone functions; (iii) We provide fast, GPU-accelerated solvers for linear and nonlinear VQR which maintain a fixed memory footprint with number of samples and quantile levels, and demonstrate that they scale to millions of samples and thousands of quantile levels; (iv) We release an optimized python package of our solvers as to widespread the use of VQR in real-world applications.

Joint optimization of system design and reconstruction in MIMO radar imaging

Multiple-input multiple-output (MIMO) radar is one of the leading depth sensing modalities. However, the usage of multiple receive channels lead to relative high costs and prevent the penetration of MIMOs in many areas such as the automotive industry. Over the last years, few studies concentrated on designing reduced measurement schemes and image reconstruction schemes for MIMO radars, however these problems have been so far addressed separately. On the other hand, recent works in optical computational imaging have demonstrated growing success of simultaneous learning-based design of the acquisition and reconstruction schemes, manifesting significant improvement in the reconstruction quality. Inspired by these successes, in this work, we propose to learn MIMO acquisition parameters in the form of receive (Rx) antenna elements locations jointly with an image neural-network based reconstruction. To this end, we propose an algorithm for training the combined acquisition-reconstruction pipeline end-to-end in a differentiable way. We demonstrate the significance of using our learned acquisition parameters with and without the neural-network reconstruction.

Towards learned optimal q-space sampling in diffusion MRI

Fiber tractography is an important tool of computational neuroscience that enables reconstructing the spatial connectivity and organization of white matter of the brain. Fiber tractography takes advantage of diffusion Magnetic Resonance Imaging (dMRI) which allows measuring the apparent diffusivity of cerebral water along different spatial directions. Unfortunately, collecting such data comes at the price of reduced spatial resolution and substantially elevated acquisition times, which limits the clinical applicability of dMRI. This problem has been thus far addressed using two principal strategies. Most of the efforts have been extended towards improving the quality of signal estimation for any, yet fixed sampling scheme (defined through the choice of diffusion-encoding gradients). On the other hand, optimization over the sampling scheme has also proven to be effective. Inspired by the previous results, the present work consolidates the above strategies into a unified estimation framework, in which the optimization is carried out with respect to both estimation model and sampling design {\it concurrently}. The proposed solution offers substantial improvements in the quality of signal estimation as well as the accuracy of ensuing analysis by means of fiber tractography. While proving the optimality of the learned estimation models would probably need more extensive evaluation, we nevertheless claim that the learned sampling schemes can be of immediate use, offering a way to improve the dMRI analysis without the necessity of deploying the neural network used for their estimation. We present a comprehensive comparative analysis based on the Human Connectome Project data. Code and learned sampling designs aviliable at https://github.com/tomer196/Learned_dMRI.

3D FLAT: Feasible Learned Acquisition Trajectories for Accelerated MRI

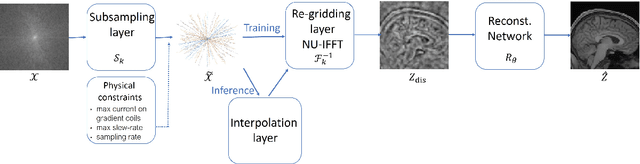
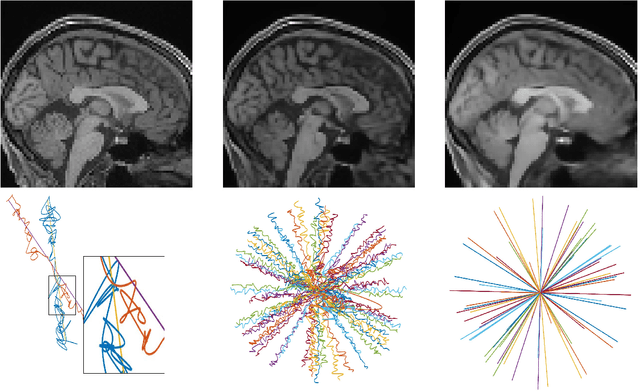
Magnetic Resonance Imaging (MRI) has long been considered to be among the gold standards of today's diagnostic imaging. The most significant drawback of MRI is long acquisition times, prohibiting its use in standard practice for some applications. Compressed sensing (CS) proposes to subsample the k-space (the Fourier domain dual to the physical space of spatial coordinates) leading to significantly accelerated acquisition. However, the benefit of compressed sensing has not been fully exploited; most of the sampling densities obtained through CS do not produce a trajectory that obeys the stringent constraints of the MRI machine imposed in practice. Inspired by recent success of deep learning based approaches for image reconstruction and ideas from computational imaging on learning-based design of imaging systems, we introduce 3D FLAT, a novel protocol for data-driven design of 3D non-Cartesian accelerated trajectories in MRI. Our proposal leverages the entire 3D k-space to simultaneously learn a physically feasible acquisition trajectory with a reconstruction method. Experimental results, performed as a proof-of-concept, suggest that 3D FLAT achieves higher image quality for a given readout time compared to standard trajectories such as radial, stack-of-stars, or 2D learned trajectories (trajectories that evolve only in the 2D plane while fully sampling along the third dimension). Furthermore, we demonstrate evidence supporting the significant benefit of performing MRI acquisitions using non-Cartesian 3D trajectories over 2D non-Cartesian trajectories acquired slice-wise.

Deep geometric matrix completion: Are we doing it right?

We address the problem of reconstructing a matrix from a subset of its entries. Current methods, branded as geometric matrix completion, augment classical rank regularization techniques by incorporating geometric information into the solution. This information is usually provided as graphs encoding relations between rows/columns. In this work we propose a simple spectral approach for solving the matrix completion problem, via the framework of functional maps. We introduce the zoomout loss, a multiresolution spectral geometric loss inspired by recent advances in shape correspondence, whose minimization leads to state-of-the-art results on various recommender systems datasets. Surprisingly, for some datasets we were able to achieve comparable results even without incorporating geometric information. This puts into question both the quality of such information and current methods' ability to use it in a meaningful and efficient way.