Weisfeiler and Leman Go Infinite: Spectral and Combinatorial Pre-Colorings

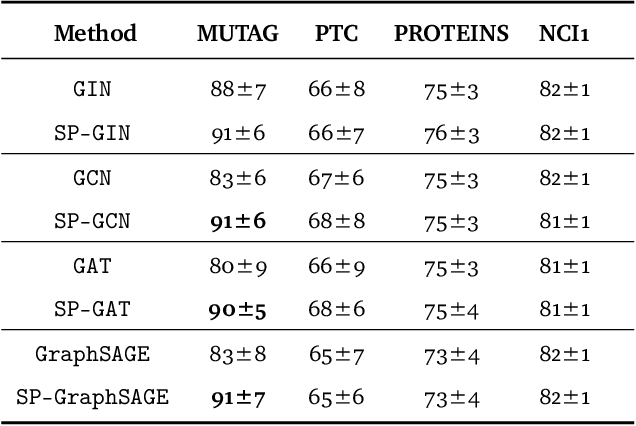
Graph isomorphism testing is usually approached via the comparison of graph invariants. Two popular alternatives that offer a good trade-off between expressive power and computational efficiency are combinatorial (i.e., obtained via the Weisfeiler-Leman (WL) test) and spectral invariants. While the exact power of the latter is still an open question, the former is regularly criticized for its limited power, when a standard configuration of uniform pre-coloring is used. This drawback hinders the applicability of Message Passing Graph Neural Networks (MPGNNs), whose expressive power is upper bounded by the WL test. Relaxing the assumption of uniform pre-coloring, we show that one can increase the expressive power of the WL test ad infinitum. Following that, we propose an efficient pre-coloring based on spectral features that provably increase the expressive power of the vanilla WL test. The above claims are accompanied by extensive synthetic and real data experiments. The code to reproduce our experiments is available at https://github.com/TPFI22/Spectral-and-Combinatorial

Deep geometric matrix completion: Are we doing it right?

We address the problem of reconstructing a matrix from a subset of its entries. Current methods, branded as geometric matrix completion, augment classical rank regularization techniques by incorporating geometric information into the solution. This information is usually provided as graphs encoding relations between rows/columns. In this work we propose a simple spectral approach for solving the matrix completion problem, via the framework of functional maps. We introduce the zoomout loss, a multiresolution spectral geometric loss inspired by recent advances in shape correspondence, whose minimization leads to state-of-the-art results on various recommender systems datasets. Surprisingly, for some datasets we were able to achieve comparable results even without incorporating geometric information. This puts into question both the quality of such information and current methods' ability to use it in a meaningful and efficient way.

Efficient Deformable Shape Correspondence via Kernel Matching

We present a method to match three dimensional shapes under non-isometric deformations, topology changes and partiality. We formulate the problem as matching between a set of pair-wise and point-wise descriptors, imposing a continuity prior on the mapping, and propose a projected descent optimization procedure inspired by difference of convex functions (DC) programming. Surprisingly, in spite of the highly non-convex nature of the resulting quadratic assignment problem, our method converges to a semantically meaningful and continuous mapping in most of our experiments, and scales well. We provide preliminary theoretical analysis and several interpretations of the method.

Inspiring Computer Vision System Solutions

The "digital Michelangelo project" was a seminal computer vision project in the early 2000's that pushed the capabilities of acquisition systems and involved multiple people from diverse fields, many of whom are now leaders in industry and academia. Reviewing this project with modern eyes provides us with the opportunity to reflect on several issues, relevant now as then to the field of computer vision and research in general, that go beyond the technical aspects of the work. This article was written in the context of a reading group competition at the week-long International Computer Vision Summer School 2017 (ICVSS) on Sicily, Italy. To deepen the participants understanding of computer vision and to foster a sense of community, various reading groups were tasked to highlight important lessons which may be learned from provided literature, going beyond the contents of the paper. This report is the winning entry of this guided discourse (Fig. 1). The authors closely examined the origins, fruits and most importantly lessons about research in general which may be distilled from the "digital Michelangelo project". Discussions leading to this report were held within the group as well as with Hao Li, the group mentor.