Efficient Deformable Shape Correspondence via Kernel Matching

We present a method to match three dimensional shapes under non-isometric deformations, topology changes and partiality. We formulate the problem as matching between a set of pair-wise and point-wise descriptors, imposing a continuity prior on the mapping, and propose a projected descent optimization procedure inspired by difference of convex functions (DC) programming. Surprisingly, in spite of the highly non-convex nature of the resulting quadratic assignment problem, our method converges to a semantically meaningful and continuous mapping in most of our experiments, and scales well. We provide preliminary theoretical analysis and several interpretations of the method.

Product Manifold Filter: Non-Rigid Shape Correspondence via Kernel Density Estimation in the Product Space

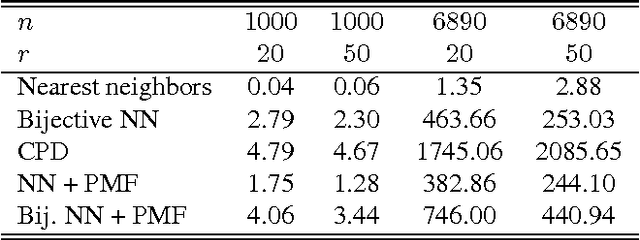
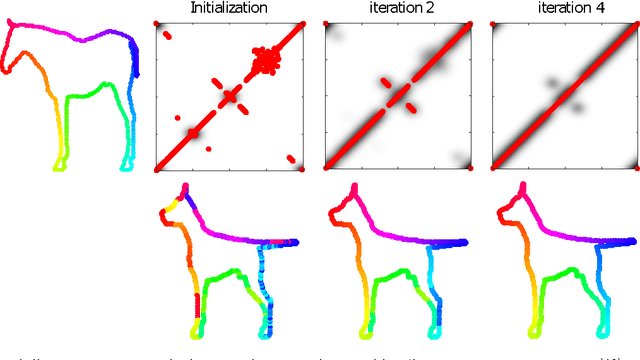
Many algorithms for the computation of correspondences between deformable shapes rely on some variant of nearest neighbor matching in a descriptor space. Such are, for example, various point-wise correspondence recovery algorithms used as a post-processing stage in the functional correspondence framework. Such frequently used techniques implicitly make restrictive assumptions (e.g., near-isometry) on the considered shapes and in practice suffer from lack of accuracy and result in poor surjectivity. We propose an alternative recovery technique capable of guaranteeing a bijective correspondence and producing significantly higher accuracy and smoothness. Unlike other methods our approach does not depend on the assumption that the analyzed shapes are isometric. We derive the proposed method from the statistical framework of kernel density estimation and demonstrate its performance on several challenging deformable 3D shape matching datasets.

Bayesian Inference of Bijective Non-Rigid Shape Correspondence

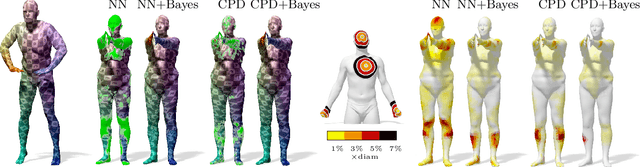
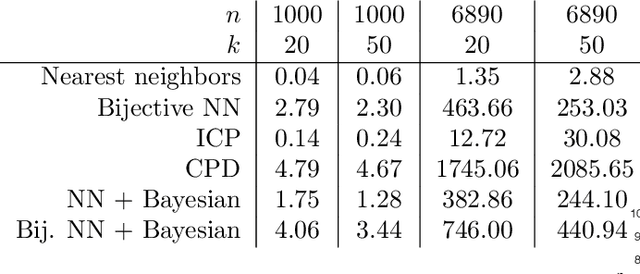
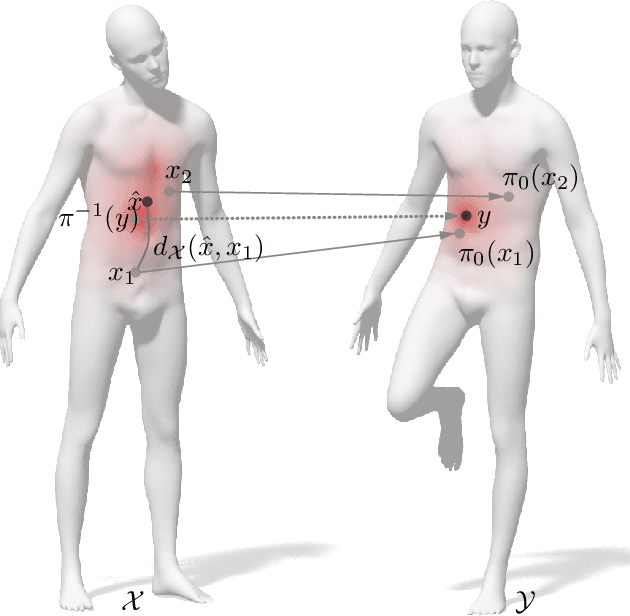
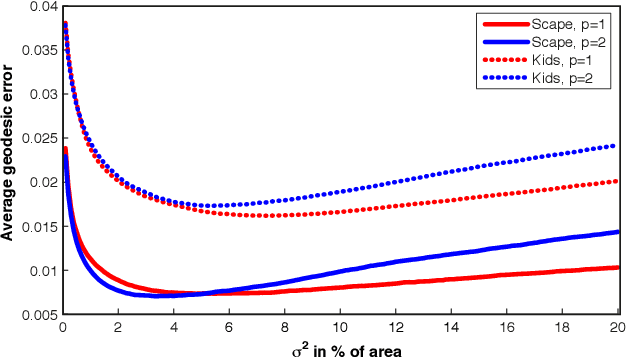
Many algorithms for the computation of correspondences between deformable shapes rely on some variant of nearest neighbor matching in a descriptor space. Such are, for example, various point-wise correspondence recovery algorithms used as a postprocessing stage in the functional correspondence framework. In this paper, we show that such frequently used techniques in practice suffer from lack of accuracy and result in poor surjectivity. We propose an alternative recovery technique guaranteeing a bijective correspondence and producing significantly higher accuracy. We derive the proposed method from a statistical framework of Bayesian inference and demonstrate its performance on several challenging deformable 3D shape matching datasets.