FLASH: Flexible Learning of Adaptive Sampling from History in Temporal Graph Neural Networks

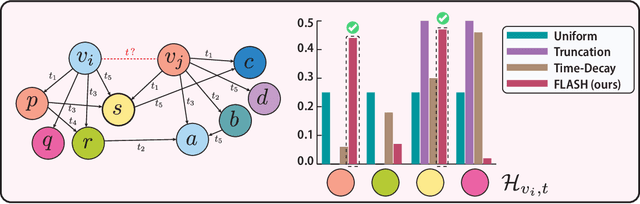
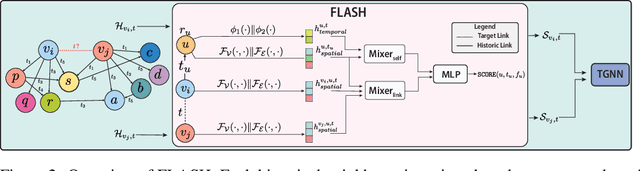
Aggregating temporal signals from historic interactions is a key step in future link prediction on dynamic graphs. However, incorporating long histories is resource-intensive. Hence, temporal graph neural networks (TGNNs) often rely on historical neighbors sampling heuristics such as uniform sampling or recent neighbors selection. These heuristics are static and fail to adapt to the underlying graph structure. We introduce FLASH, a learnable and graph-adaptive neighborhood selection mechanism that generalizes existing heuristics. FLASH integrates seamlessly into TGNNs and is trained end-to-end using a self-supervised ranking loss. We provide theoretical evidence that commonly used heuristics hinders TGNNs performance, motivating our design. Extensive experiments across multiple benchmarks demonstrate consistent and significant performance improvements for TGNNs equipped with FLASH.

Leveraging Temporal Graph Networks Using Module Decoupling

Modern approaches for learning on dynamic graphs have adopted the use of batches instead of applying updates one by one. The use of batches allows these techniques to become helpful in streaming scenarios where updates to graphs are received at extreme speeds. Using batches, however, forces the models to update infrequently, which results in the degradation of their performance. In this work, we suggest a decoupling strategy that enables the models to update frequently while using batches. By decoupling the core modules of temporal graph networks and implementing them using a minimal number of learnable parameters, we have developed the Lightweight Decoupled Temporal Graph Network (LDTGN), an exceptionally efficient model for learning on dynamic graphs. LDTG was validated on various dynamic graph benchmarks, providing comparable or state-of-the-art results with significantly higher throughput than previous art. Notably, our method outperforms previous approaches by more than 20\% on benchmarks that require rapid model update rates, such as USLegis or UNTrade. The code to reproduce our experiments is available at \href{https://orfeld415.github.io/module-decoupling}{this http url}.

Weisfeiler and Leman Go Infinite: Spectral and Combinatorial Pre-Colorings

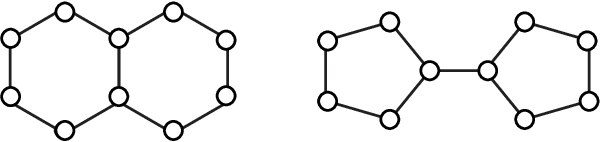
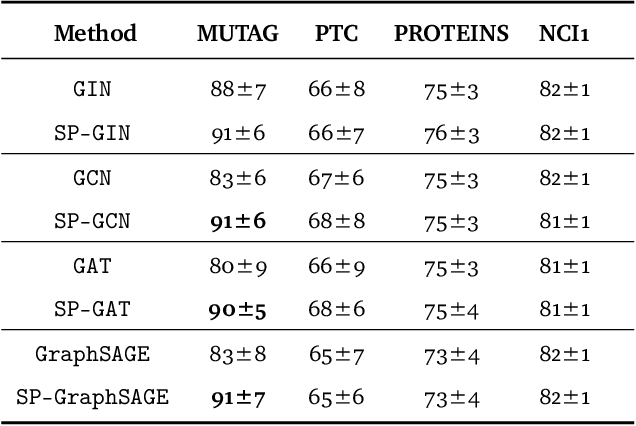
Graph isomorphism testing is usually approached via the comparison of graph invariants. Two popular alternatives that offer a good trade-off between expressive power and computational efficiency are combinatorial (i.e., obtained via the Weisfeiler-Leman (WL) test) and spectral invariants. While the exact power of the latter is still an open question, the former is regularly criticized for its limited power, when a standard configuration of uniform pre-coloring is used. This drawback hinders the applicability of Message Passing Graph Neural Networks (MPGNNs), whose expressive power is upper bounded by the WL test. Relaxing the assumption of uniform pre-coloring, we show that one can increase the expressive power of the WL test ad infinitum. Following that, we propose an efficient pre-coloring based on spectral features that provably increase the expressive power of the vanilla WL test. The above claims are accompanied by extensive synthetic and real data experiments. The code to reproduce our experiments is available at https://github.com/TPFI22/Spectral-and-Combinatorial