Automatic topography of high-dimensional data sets by non-parametric Density Peak clustering

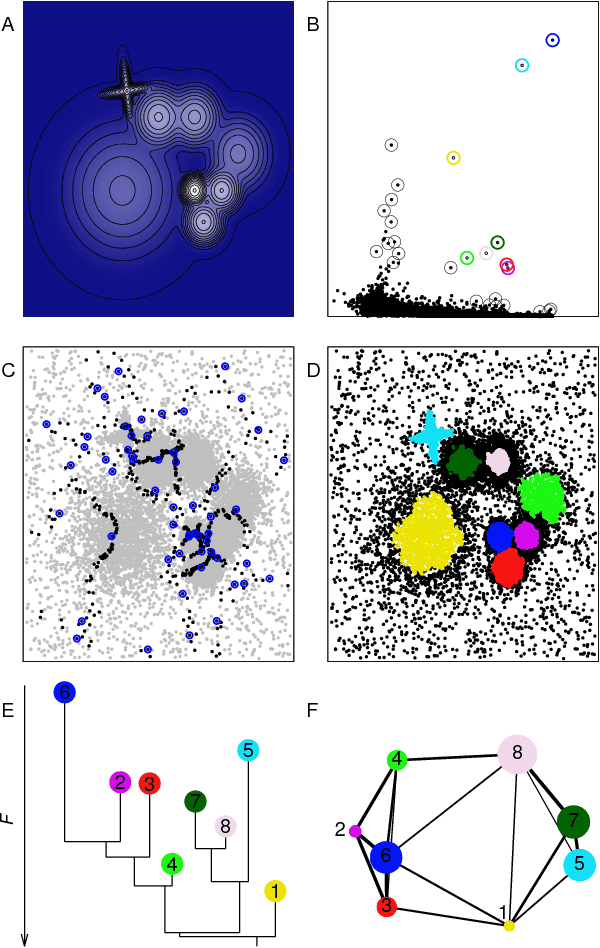
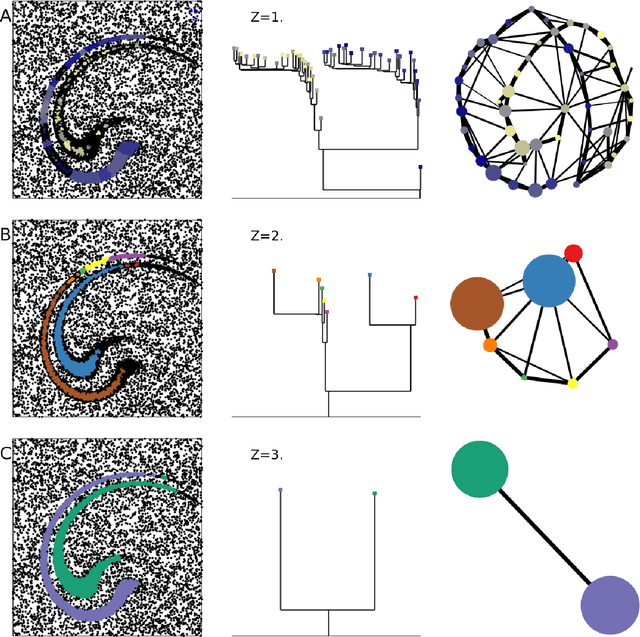
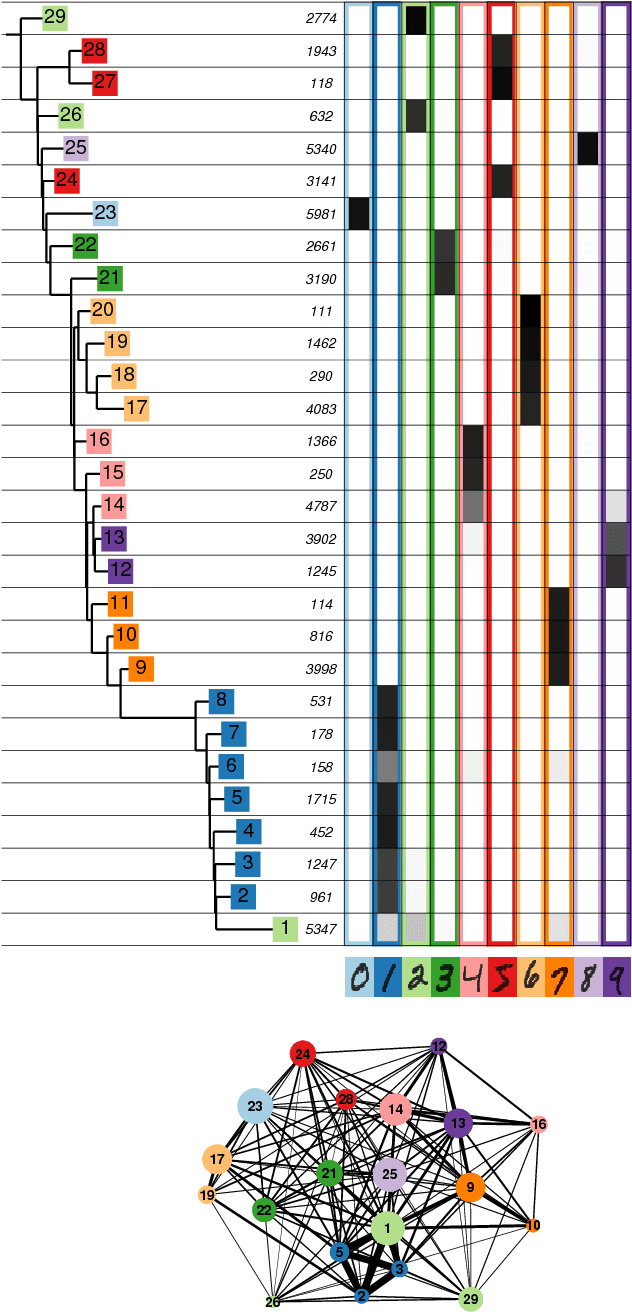
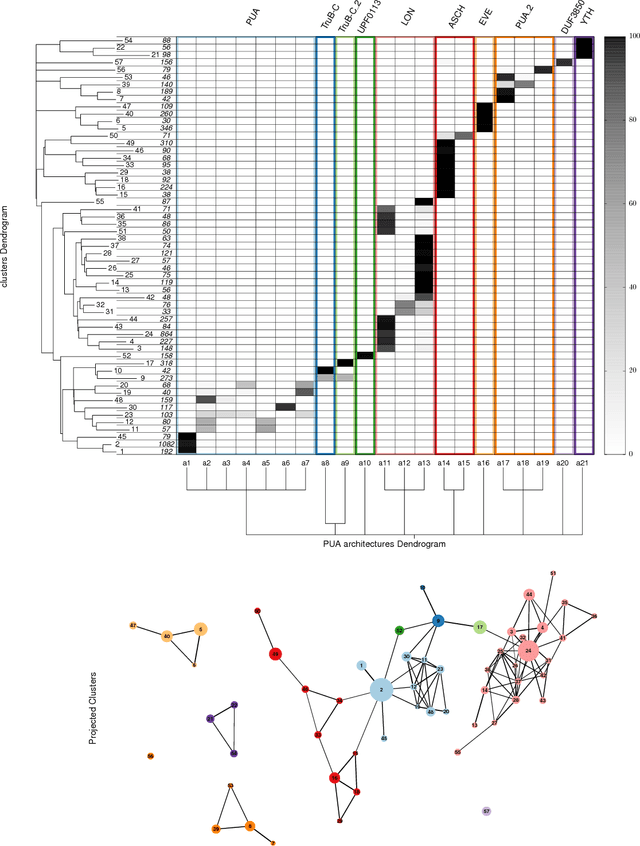
Data analysis in high-dimensional spaces aims at obtaining a synthetic description of a data set, revealing its main structure and its salient features. We here introduce an approach for charting data spaces, providing a topography of the probability distribution from which the data are harvested. This topography includes information on the number and the height of the probability peaks, the depth of the "valleys" separating them, the relative location of the peaks and their hierarchical organization. The topography is reconstructed by using an unsupervised variant of Density Peak clustering exploiting a non-parametric density estimator, which automatically measures the density in the manifold containing the data. Importantly, the density estimator provides an estimate of the error. This is a key feature, which allows distinguishing genuine probability peaks from density fluctuations due to finite sampling.