How does the brain compute with probabilities?

This perspective piece is the result of a Generative Adversarial Collaboration (GAC) tackling the question `How does neural activity represent probability distributions?'. We have addressed three major obstacles to progress on answering this question: first, we provide a unified language for defining competing hypotheses. Second, we explain the fundamentals of three prominent proposals for probabilistic computations -- Probabilistic Population Codes (PPCs), Distributed Distributional Codes (DDCs), and Neural Sampling Codes (NSCs) -- and describe similarities and differences in that common language. Third, we review key empirical data previously taken as evidence for at least one of these proposal, and describe how it may or may not be explainable by alternative proposals. Finally, we describe some key challenges in resolving the debate, and propose potential directions to address them through a combination of theory and experiments.

Control when confidence is costly

We develop a version of stochastic control that accounts for computational costs of inference. Past studies identified efficient coding without control, or efficient control that neglects the cost of synthesizing information. Here we combine these concepts into a framework where agents rationally approximate inference for efficient control. Specifically, we study Linear Quadratic Gaussian (LQG) control with an added internal cost on the relative precision of the posterior probability over the world state. This creates a trade-off: an agent can obtain more utility overall by sacrificing some task performance, if doing so saves enough bits during inference. We discover that the rational strategy that solves the joint inference and control problem goes through phase transitions depending on the task demands, switching from a costly but optimal inference to a family of suboptimal inferences related by rotation transformations, each misestimate the stability of the world. In all cases, the agent moves more to think less. This work provides a foundation for a new type of rational computations that could be used by both brains and machines for efficient but computationally constrained control.

Generalization properties of contrastive world models

Recent work on object-centric world models aim to factorize representations in terms of objects in a completely unsupervised or self-supervised manner. Such world models are hypothesized to be a key component to address the generalization problem. While self-supervision has shown improved performance however, OOD generalization has not been systematically and explicitly tested. In this paper, we conduct an extensive study on the generalization properties of contrastive world model. We systematically test the model under a number of different OOD generalization scenarios such as extrapolation to new object attributes, introducing new conjunctions or new attributes. Our experiments show that the contrastive world model fails to generalize under the different OOD tests and the drop in performance depends on the extent to which the samples are OOD. When visualizing the transition updates and convolutional feature maps, we observe that any changes in object attributes (such as previously unseen colors, shapes, or conjunctions of color and shape) breaks down the factorization of object representations. Overall, our work highlights the importance of object-centric representations for generalization and current models are limited in their capacity to learn such representations required for human-level generalization.

Inferring Inference

Patterns of microcircuitry suggest that the brain has an array of repeated canonical computational units. Yet neural representations are distributed, so the relevant computations may only be related indirectly to single-neuron transformations. It thus remains an open challenge how to define canonical distributed computations. We integrate normative and algorithmic theories of neural computation into a mathematical framework for inferring canonical distributed computations from large-scale neural activity patterns. At the normative level, we hypothesize that the brain creates a structured internal model of its environment, positing latent causes that explain its sensory inputs, and uses those sensory inputs to infer the latent causes. At the algorithmic level, we propose that this inference process is a nonlinear message-passing algorithm on a graph-structured model of the world. Given a time series of neural activity during a perceptual inference task, our framework finds (i) the neural representation of relevant latent variables, (ii) interactions between these variables that define the brain's internal model of the world, and (iii) message-functions specifying the inference algorithm. These targeted computational properties are then statistically distinguishable due to the symmetries inherent in any canonical computation, up to a global transformation. As a demonstration, we simulate recordings for a model brain that implicitly implements an approximate inference algorithm on a probabilistic graphical model. Given its external inputs and noisy neural activity, we recover the latent variables, their neural representation and dynamics, and canonical message-functions. We highlight features of experimental design needed to successfully extract canonical computations from neural data. Overall, this framework provides a new tool for discovering interpretable structure in neural recordings.

Understanding robustness and generalization of artificial neural networks through Fourier masks

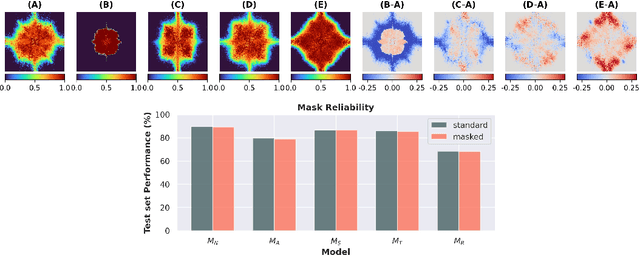
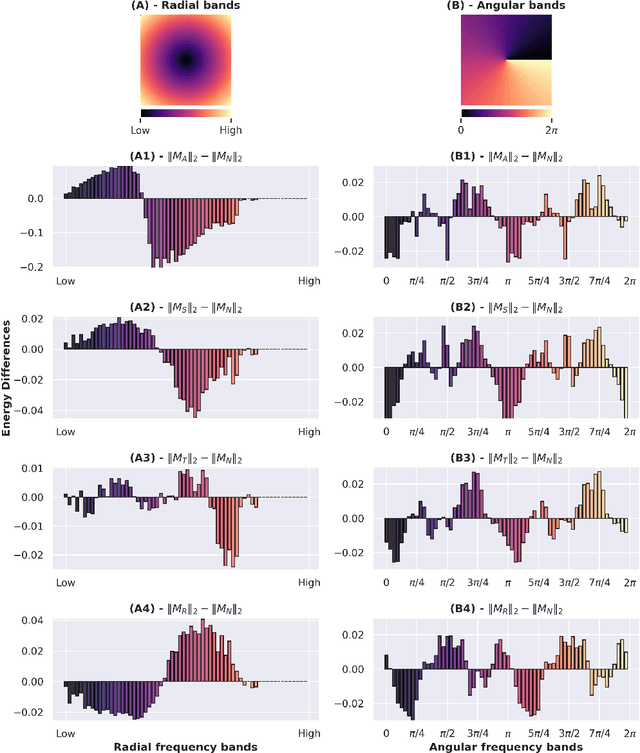
Despite the enormous success of artificial neural networks (ANNs) in many disciplines, the characterization of their computations and the origin of key properties such as generalization and robustness remain open questions. Recent literature suggests that robust networks with good generalization properties tend to be biased towards processing low frequencies in images. To explore the frequency bias hypothesis further, we develop an algorithm that allows us to learn modulatory masks highlighting the essential input frequencies needed for preserving a trained network's performance. We achieve this by imposing invariance in the loss with respect to such modulations in the input frequencies. We first use our method to test the low-frequency preference hypothesis of adversarially trained or data-augmented networks. Our results suggest that adversarially robust networks indeed exhibit a low-frequency bias but we find this bias is also dependent on directions in frequency space. However, this is not necessarily true for other types of data augmentation. Our results also indicate that the essential frequencies in question are effectively the ones used to achieve generalization in the first place. Surprisingly, images seen through these modulatory masks are not recognizable and resemble texture-like patterns.

Learning Dynamics and Structure of Complex Systems Using Graph Neural Networks

Many complex systems are composed of interacting parts, and the underlying laws are usually simple and universal. While graph neural networks provide a useful relational inductive bias for modeling such systems, generalization to new system instances of the same type is less studied. In this work we trained graph neural networks to fit time series from an example nonlinear dynamical system, the belief propagation algorithm. We found simple interpretations of the learned representation and model components, and they are consistent with core properties of the probabilistic inference algorithm. We successfully identified a `graph translator' between the statistical interactions in belief propagation and parameters of the corresponding trained network, and showed that it enables two types of novel generalization: to recover the underlying structure of a new system instance based solely on time series observations, or to construct a new network from this structure directly. Our results demonstrated a path towards understanding both dynamics and structure of a complex system and how such understanding can be used for generalization.

Interpolating between sampling and variational inference with infinite stochastic mixtures

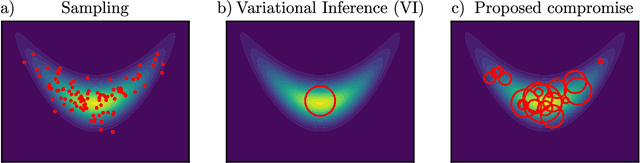
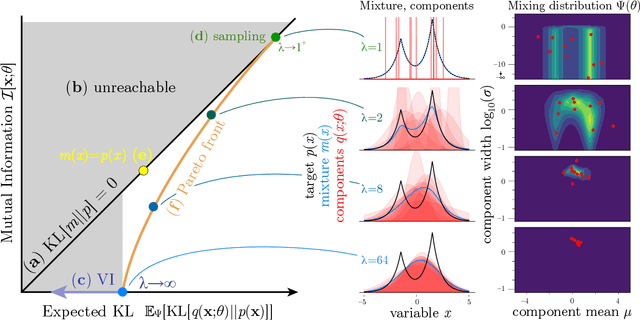
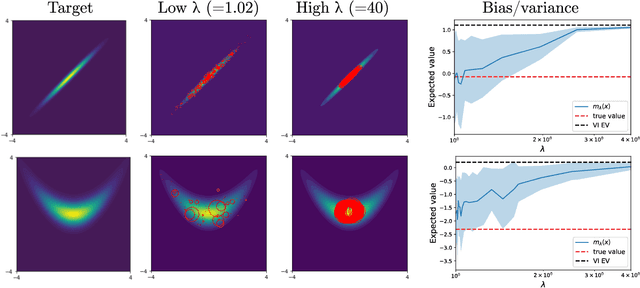
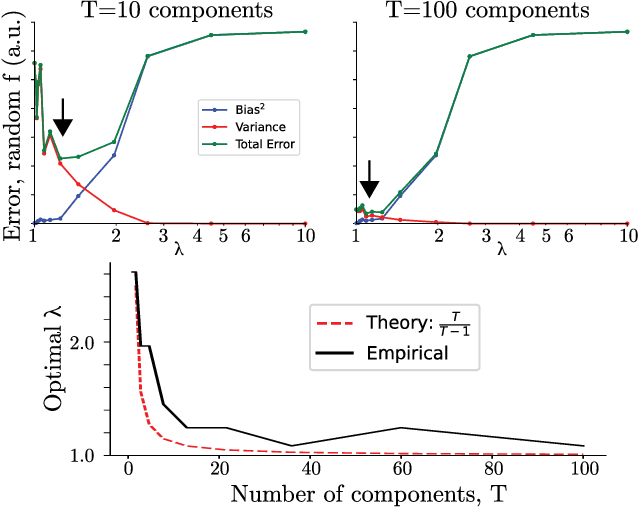
Sampling and Variational Inference (VI) are two large families of methods for approximate inference with complementary strengths. Sampling methods excel at approximating arbitrary probability distributions, but can be inefficient. VI methods are efficient, but can fail when probability distributions are complex. Here, we develop a framework for constructing intermediate algorithms that balance the strengths of both sampling and VI. Both approximate a probability distribution using a mixture of simple component distributions: in sampling, each component is a delta-function and is chosen stochastically, while in standard VI a single component is chosen to minimize divergence. We show that sampling and VI emerge as special cases of an optimization problem over a mixing distribution, and intermediate approximations arise by varying a single parameter. We then derive closed-form sampling dynamics over variational parameters that stochastically build a mixture. Finally, we discuss how to select the optimal compromise between sampling and VI given a computational budget. This work is a first step towards a highly flexible yet simple family of inference methods that combines the complementary strengths of sampling and VI.

Two-argument activation functions learn soft XOR operations like cortical neurons

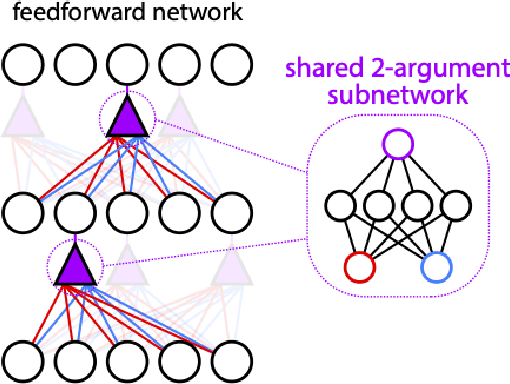
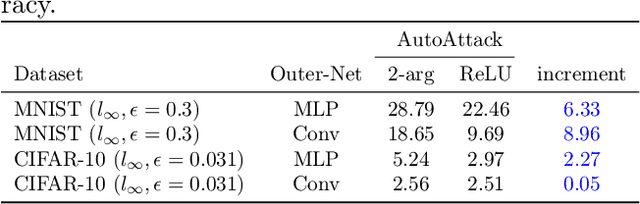
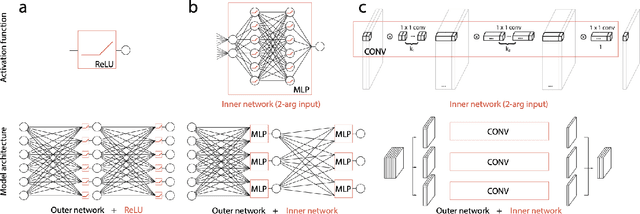
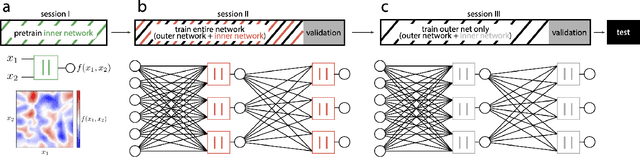
Neurons in the brain are complex machines with distinct functional compartments that interact nonlinearly. In contrast, neurons in artificial neural networks abstract away this complexity, typically down to a scalar activation function of a weighted sum of inputs. Here we emulate more biologically realistic neurons by learning canonical activation functions with two input arguments, analogous to basal and apical dendrites. We use a network-in-network architecture where each neuron is modeled as a multilayer perceptron with two inputs and a single output. This inner perceptron is shared by all units in the outer network. Remarkably, the resultant nonlinearities often produce soft XOR functions, consistent with recent experimental observations about interactions between inputs in human cortical neurons. When hyperparameters are optimized, networks with these nonlinearities learn faster and perform better than conventional ReLU nonlinearities with matched parameter counts, and they are more robust to natural and adversarial perturbations.

Generalization of graph network inferences in higher-order probabilistic graphical models

Probabilistic graphical models provide a powerful tool to describe complex statistical structure, with many real-world applications in science and engineering from controlling robotic arms to understanding neuronal computations. A major challenge for these graphical models is that inferences such as marginalization are intractable for general graphs. These inferences are often approximated by a distributed message-passing algorithm such as Belief Propagation, which does not always perform well on graphs with cycles, nor can it always be easily specified for complex continuous probability distributions. Such difficulties arise frequently in expressive graphical models that include intractable higher-order interactions. In this paper we construct iterative message-passing algorithms using Graph Neural Networks defined on factor graphs to achieve fast approximate inference on graphical models that involve many-variable interactions. Experimental results on several families of graphical models demonstrate the out-of-distribution generalization capability of our method to different sized graphs, and indicate the domain in which our method gains advantage over Belief Propagation.

AvaTr: One-Shot Speaker Extraction with Transformers

To extract the voice of a target speaker when mixed with a variety of other sounds, such as white and ambient noises or the voices of interfering speakers, we extend the Transformer network to attend the most relevant information with respect to the target speaker given the characteristics of his or her voices as a form of contextual information. The idea has a natural interpretation in terms of the selective attention theory. Specifically, we propose two models to incorporate the voice characteristics in Transformer based on different insights of where the feature selection should take place. Both models yield excellent performance, on par or better than published state-of-the-art models on the speaker extraction task, including separating speech of novel speakers not seen during training.