A large language model-assisted education tool to provide feedback on open-ended responses

Open-ended questions are a favored tool among instructors for assessing student understanding and encouraging critical exploration of course material. Providing feedback for such responses is a time-consuming task that can lead to overwhelmed instructors and decreased feedback quality. Many instructors resort to simpler question formats, like multiple-choice questions, which provide immediate feedback but at the expense of personalized and insightful comments. Here, we present a tool that uses large language models (LLMs), guided by instructor-defined criteria, to automate responses to open-ended questions. Our tool delivers rapid personalized feedback, enabling students to quickly test their knowledge and identify areas for improvement. We provide open-source reference implementations both as a web application and as a Jupyter Notebook widget that can be used with instructional coding or math notebooks. With instructor guidance, LLMs hold promise to enhance student learning outcomes and elevate instructional methodologies.

Neural Networks as Paths through the Space of Representations

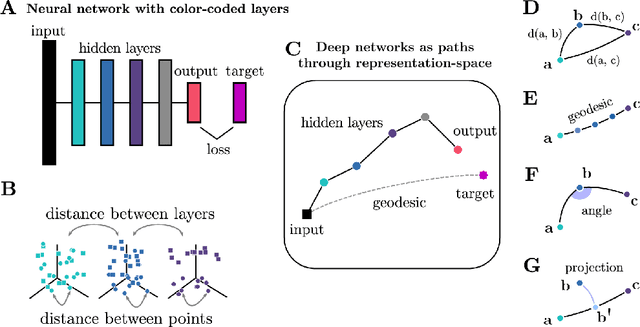
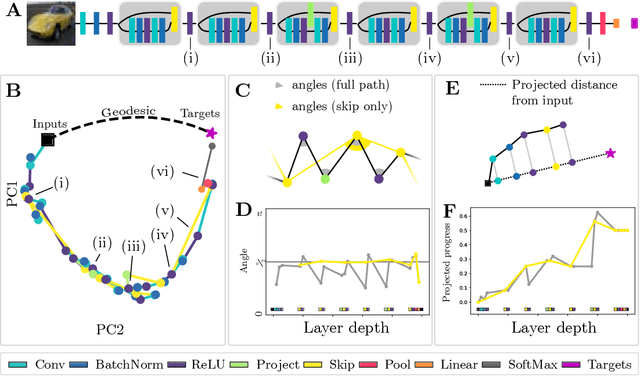
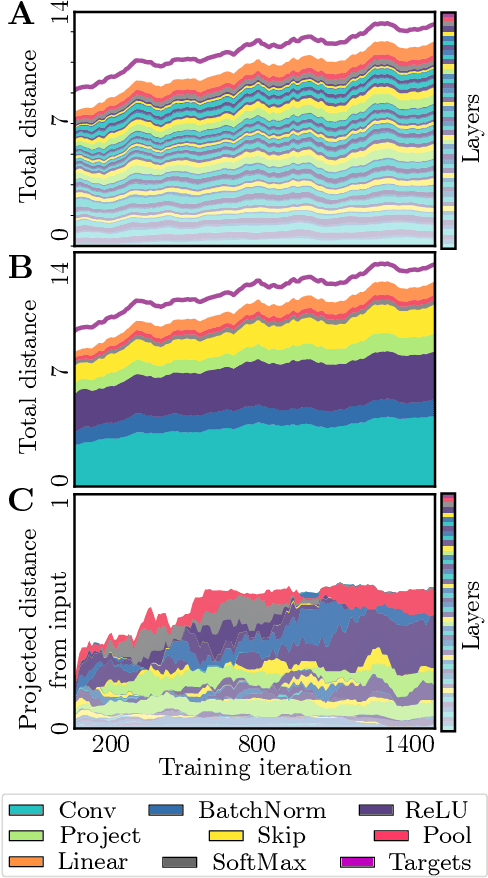
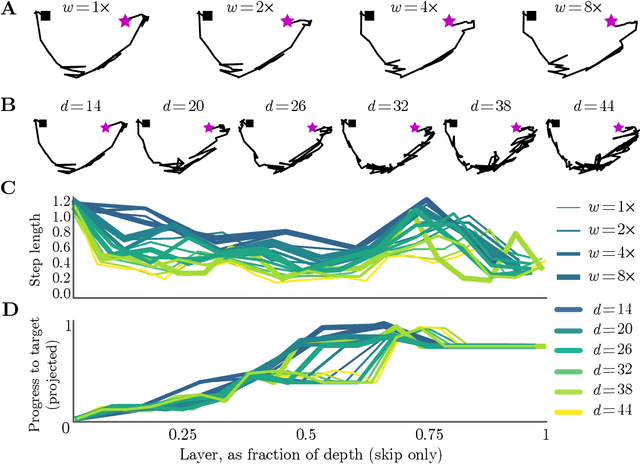
Deep neural networks implement a sequence of layer-by-layer operations that are each relatively easy to understand, but the resulting overall computation is generally difficult to understand. We develop a simple idea for interpreting the layer-by-layer construction of useful representations: the role of each layer is to reformat information to reduce the "distance" to the target outputs. We formalize this intuitive idea of "distance" by leveraging recent work on metric representational similarity, and show how it leads to a rich space of geometric concepts. With this framework, the layer-wise computation implemented by a deep neural network can be viewed as a path in a high-dimensional representation space. We develop tools to characterize the geometry of these in terms of distances, angles, and geodesics. We then ask three sets of questions of residual networks trained on CIFAR-10: (1) how straight are paths, and how does each layer contribute towards the target? (2) how do these properties emerge over training? and (3) how similar are the paths taken by wider versus deeper networks? We conclude by sketching additional ways that this kind of representational geometry can be used to understand and interpret network training, or to prescriptively improve network architectures to suit a task.

Clustering units in neural networks: upstream vs downstream information

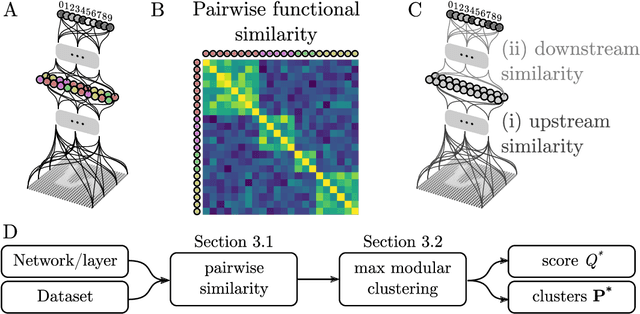
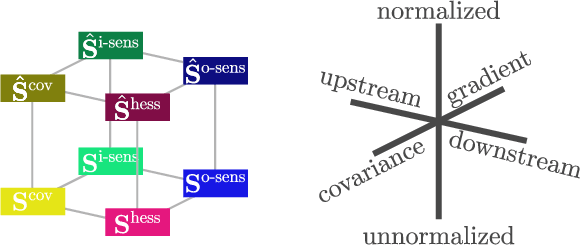
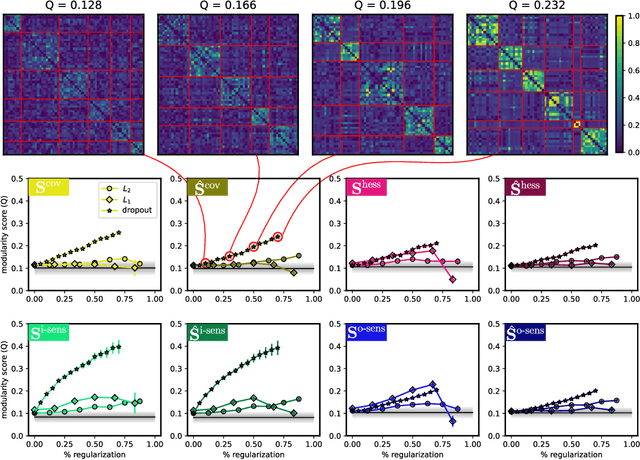
It has been hypothesized that some form of "modular" structure in artificial neural networks should be useful for learning, compositionality, and generalization. However, defining and quantifying modularity remains an open problem. We cast the problem of detecting functional modules into the problem of detecting clusters of similar-functioning units. This begs the question of what makes two units functionally similar. For this, we consider two broad families of methods: those that define similarity based on how units respond to structured variations in inputs ("upstream"), and those based on how variations in hidden unit activations affect outputs ("downstream"). We conduct an empirical study quantifying modularity of hidden layer representations of simple feedforward, fully connected networks, across a range of hyperparameters. For each model, we quantify pairwise associations between hidden units in each layer using a variety of both upstream and downstream measures, then cluster them by maximizing their "modularity score" using established tools from network science. We find two surprising results: first, dropout dramatically increased modularity, while other forms of weight regularization had more modest effects. Second, although we observe that there is usually good agreement about clusters within both upstream methods and downstream methods, there is little agreement about the cluster assignments across these two families of methods. This has important implications for representation-learning, as it suggests that finding modular representations that reflect structure in inputs (e.g. disentanglement) may be a distinct goal from learning modular representations that reflect structure in outputs (e.g. compositionality).

Interpolating between sampling and variational inference with infinite stochastic mixtures

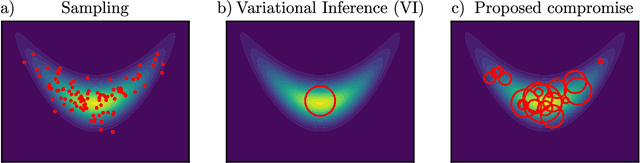
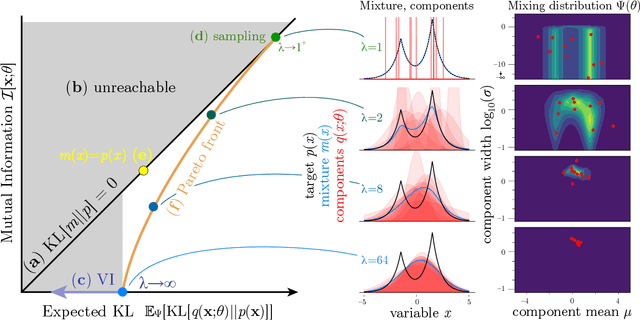
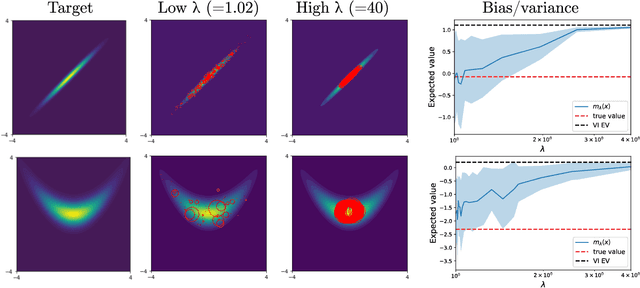
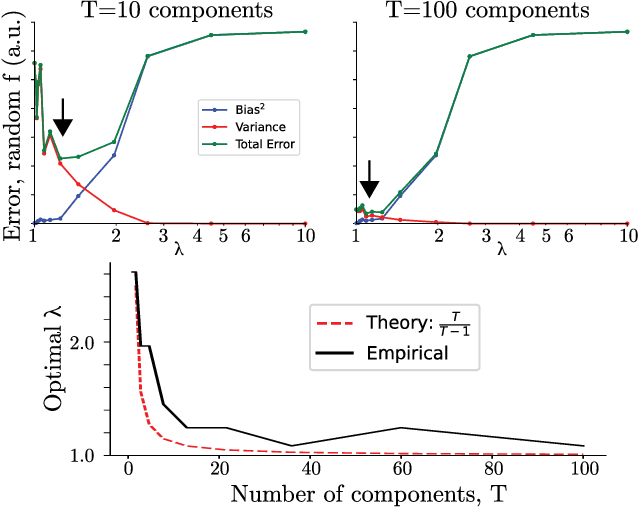
Sampling and Variational Inference (VI) are two large families of methods for approximate inference with complementary strengths. Sampling methods excel at approximating arbitrary probability distributions, but can be inefficient. VI methods are efficient, but can fail when probability distributions are complex. Here, we develop a framework for constructing intermediate algorithms that balance the strengths of both sampling and VI. Both approximate a probability distribution using a mixture of simple component distributions: in sampling, each component is a delta-function and is chosen stochastically, while in standard VI a single component is chosen to minimize divergence. We show that sampling and VI emerge as special cases of an optimization problem over a mixing distribution, and intermediate approximations arise by varying a single parameter. We then derive closed-form sampling dynamics over variational parameters that stochastically build a mixture. Finally, we discuss how to select the optimal compromise between sampling and VI given a computational budget. This work is a first step towards a highly flexible yet simple family of inference methods that combines the complementary strengths of sampling and VI.