Clustering units in neural networks: upstream vs downstream information
Paper and Code
Mar 22, 2022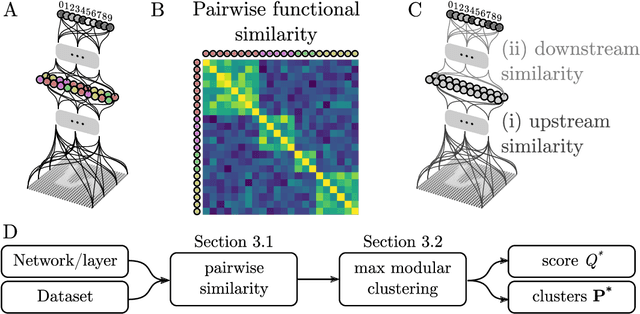
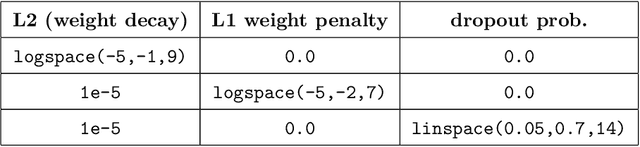
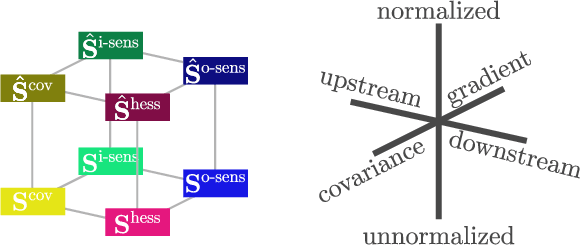
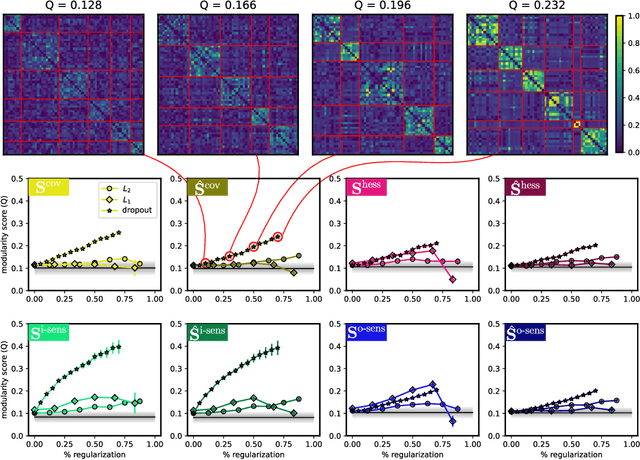
It has been hypothesized that some form of "modular" structure in artificial neural networks should be useful for learning, compositionality, and generalization. However, defining and quantifying modularity remains an open problem. We cast the problem of detecting functional modules into the problem of detecting clusters of similar-functioning units. This begs the question of what makes two units functionally similar. For this, we consider two broad families of methods: those that define similarity based on how units respond to structured variations in inputs ("upstream"), and those based on how variations in hidden unit activations affect outputs ("downstream"). We conduct an empirical study quantifying modularity of hidden layer representations of simple feedforward, fully connected networks, across a range of hyperparameters. For each model, we quantify pairwise associations between hidden units in each layer using a variety of both upstream and downstream measures, then cluster them by maximizing their "modularity score" using established tools from network science. We find two surprising results: first, dropout dramatically increased modularity, while other forms of weight regularization had more modest effects. Second, although we observe that there is usually good agreement about clusters within both upstream methods and downstream methods, there is little agreement about the cluster assignments across these two families of methods. This has important implications for representation-learning, as it suggests that finding modular representations that reflect structure in inputs (e.g. disentanglement) may be a distinct goal from learning modular representations that reflect structure in outputs (e.g. compositionality).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge