Neural Networks as Paths through the Space of Representations
Paper and Code
Jun 22, 2022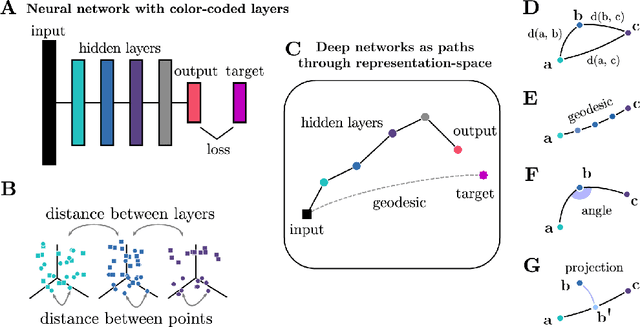
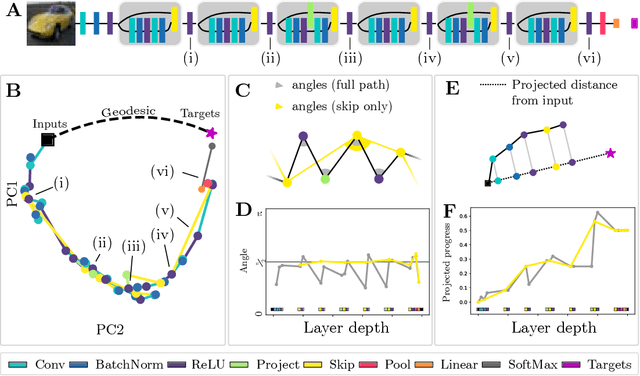
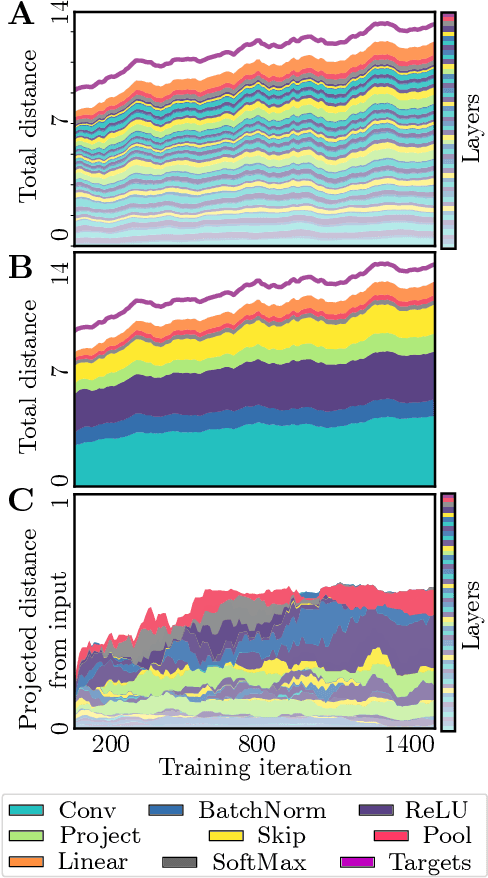
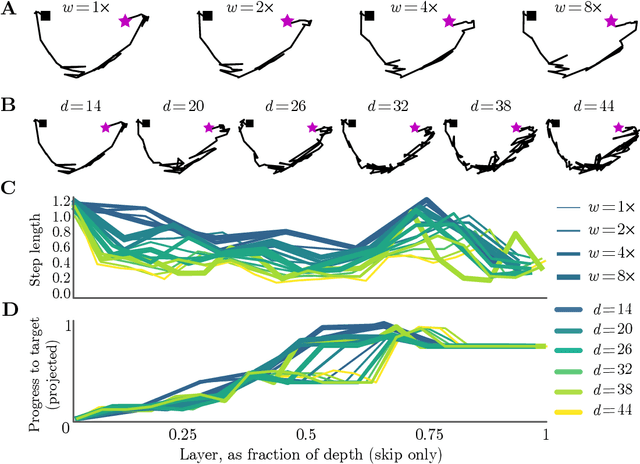
Deep neural networks implement a sequence of layer-by-layer operations that are each relatively easy to understand, but the resulting overall computation is generally difficult to understand. We develop a simple idea for interpreting the layer-by-layer construction of useful representations: the role of each layer is to reformat information to reduce the "distance" to the target outputs. We formalize this intuitive idea of "distance" by leveraging recent work on metric representational similarity, and show how it leads to a rich space of geometric concepts. With this framework, the layer-wise computation implemented by a deep neural network can be viewed as a path in a high-dimensional representation space. We develop tools to characterize the geometry of these in terms of distances, angles, and geodesics. We then ask three sets of questions of residual networks trained on CIFAR-10: (1) how straight are paths, and how does each layer contribute towards the target? (2) how do these properties emerge over training? and (3) how similar are the paths taken by wider versus deeper networks? We conclude by sketching additional ways that this kind of representational geometry can be used to understand and interpret network training, or to prescriptively improve network architectures to suit a task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge