Simultaneous linear connectivity of neural networks modulo permutation

Neural networks typically exhibit permutation symmetries which contribute to the non-convexity of the networks' loss landscapes, since linearly interpolating between two permuted versions of a trained network tends to encounter a high loss barrier. Recent work has argued that permutation symmetries are the only sources of non-convexity, meaning there are essentially no such barriers between trained networks if they are permuted appropriately. In this work, we refine these arguments into three distinct claims of increasing strength. We show that existing evidence only supports "weak linear connectivity"-that for each pair of networks belonging to a set of SGD solutions, there exist (multiple) permutations that linearly connect it with the other networks. In contrast, the claim "strong linear connectivity"-that for each network, there exists one permutation that simultaneously connects it with the other networks-is both intuitively and practically more desirable. This stronger claim would imply that the loss landscape is convex after accounting for permutation, and enable linear interpolation between three or more independently trained models without increased loss. In this work, we introduce an intermediate claim-that for certain sequences of networks, there exists one permutation that simultaneously aligns matching pairs of networks from these sequences. Specifically, we discover that a single permutation aligns sequences of iteratively trained as well as iteratively pruned networks, meaning that two networks exhibit low loss barriers at each step of their optimization and sparsification trajectories respectively. Finally, we provide the first evidence that strong linear connectivity may be possible under certain conditions, by showing that barriers decrease with increasing network width when interpolating among three networks.

Dataset Difficulty and the Role of Inductive Bias

Motivated by the goals of dataset pruning and defect identification, a growing body of methods have been developed to score individual examples within a dataset. These methods, which we call "example difficulty scores", are typically used to rank or categorize examples, but the consistency of rankings between different training runs, scoring methods, and model architectures is generally unknown. To determine how example rankings vary due to these random and controlled effects, we systematically compare different formulations of scores over a range of runs and model architectures. We find that scores largely share the following traits: they are noisy over individual runs of a model, strongly correlated with a single notion of difficulty, and reveal examples that range from being highly sensitive to insensitive to the inductive biases of certain model architectures. Drawing from statistical genetics, we develop a simple method for fingerprinting model architectures using a few sensitive examples. These findings guide practitioners in maximizing the consistency of their scores (e.g. by choosing appropriate scoring methods, number of runs, and subsets of examples), and establishes comprehensive baselines for evaluating scores in the future.

Neural Networks as Paths through the Space of Representations

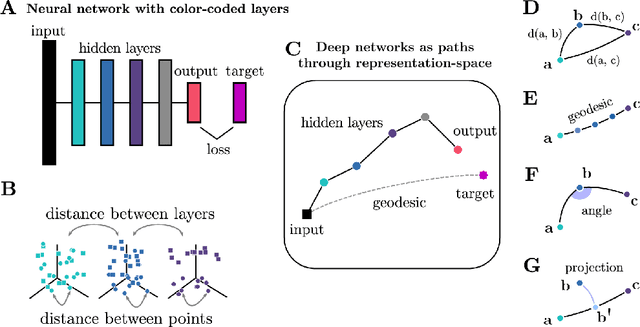
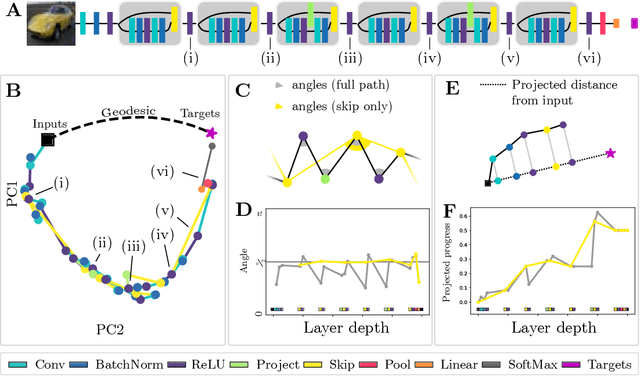
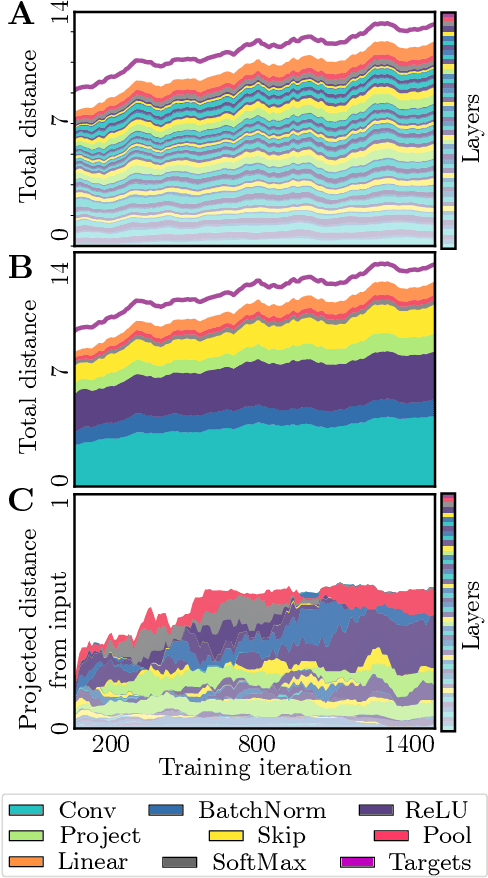
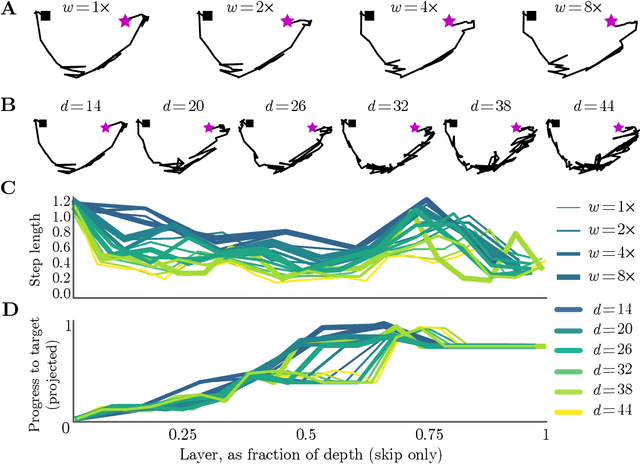
Deep neural networks implement a sequence of layer-by-layer operations that are each relatively easy to understand, but the resulting overall computation is generally difficult to understand. We develop a simple idea for interpreting the layer-by-layer construction of useful representations: the role of each layer is to reformat information to reduce the "distance" to the target outputs. We formalize this intuitive idea of "distance" by leveraging recent work on metric representational similarity, and show how it leads to a rich space of geometric concepts. With this framework, the layer-wise computation implemented by a deep neural network can be viewed as a path in a high-dimensional representation space. We develop tools to characterize the geometry of these in terms of distances, angles, and geodesics. We then ask three sets of questions of residual networks trained on CIFAR-10: (1) how straight are paths, and how does each layer contribute towards the target? (2) how do these properties emerge over training? and (3) how similar are the paths taken by wider versus deeper networks? We conclude by sketching additional ways that this kind of representational geometry can be used to understand and interpret network training, or to prescriptively improve network architectures to suit a task.