How does the brain compute with probabilities?

This perspective piece is the result of a Generative Adversarial Collaboration (GAC) tackling the question `How does neural activity represent probability distributions?'. We have addressed three major obstacles to progress on answering this question: first, we provide a unified language for defining competing hypotheses. Second, we explain the fundamentals of three prominent proposals for probabilistic computations -- Probabilistic Population Codes (PPCs), Distributed Distributional Codes (DDCs), and Neural Sampling Codes (NSCs) -- and describe similarities and differences in that common language. Third, we review key empirical data previously taken as evidence for at least one of these proposal, and describe how it may or may not be explainable by alternative proposals. Finally, we describe some key challenges in resolving the debate, and propose potential directions to address them through a combination of theory and experiments.

Interpolating between sampling and variational inference with infinite stochastic mixtures

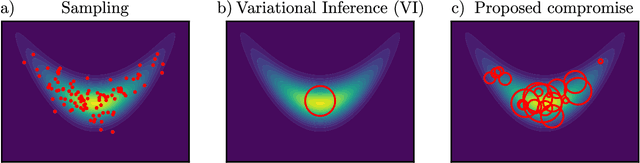
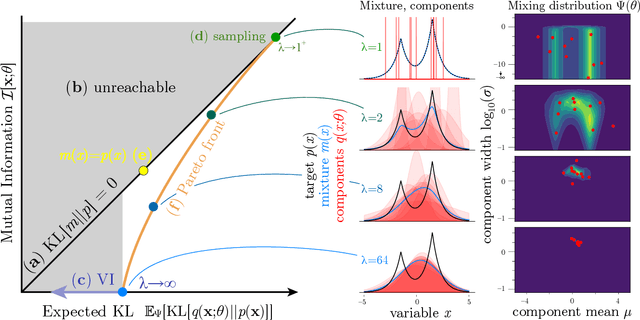
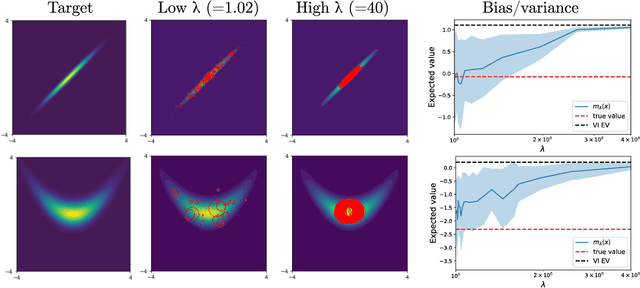
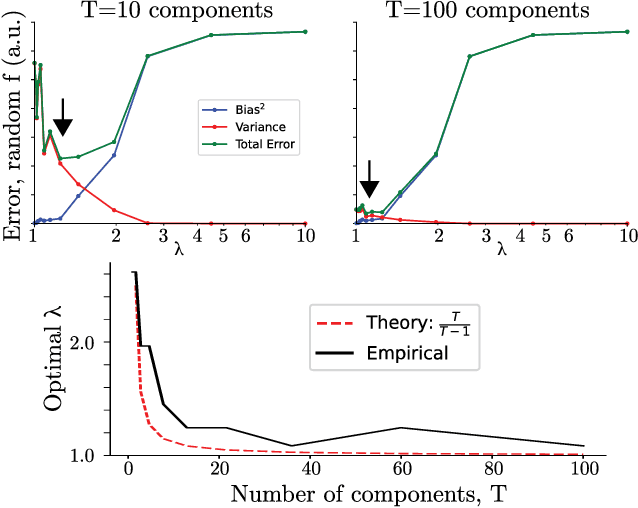
Sampling and Variational Inference (VI) are two large families of methods for approximate inference with complementary strengths. Sampling methods excel at approximating arbitrary probability distributions, but can be inefficient. VI methods are efficient, but can fail when probability distributions are complex. Here, we develop a framework for constructing intermediate algorithms that balance the strengths of both sampling and VI. Both approximate a probability distribution using a mixture of simple component distributions: in sampling, each component is a delta-function and is chosen stochastically, while in standard VI a single component is chosen to minimize divergence. We show that sampling and VI emerge as special cases of an optimization problem over a mixing distribution, and intermediate approximations arise by varying a single parameter. We then derive closed-form sampling dynamics over variational parameters that stochastically build a mixture. Finally, we discuss how to select the optimal compromise between sampling and VI given a computational budget. This work is a first step towards a highly flexible yet simple family of inference methods that combines the complementary strengths of sampling and VI.