The Spectral Bias of Shallow Neural Network Learning is Shaped by the Choice of Non-linearity

Despite classical statistical theory predicting severe overfitting, modern massively overparameterized neural networks still generalize well. This unexpected property is attributed to the network's so-called implicit bias, which describes its propensity to converge to solutions that generalize effectively, among the many possible that correctly label the training data. The aim of our research is to explore this bias from a new perspective, focusing on how non-linear activation functions contribute to shaping it. First, we introduce a reparameterization which removes a continuous weight rescaling symmetry. Second, in the kernel regime, we leverage this reparameterization to generalize recent findings that relate shallow Neural Networks to the Radon transform, deriving an explicit formula for the implicit bias induced by a broad class of activation functions. Specifically, by utilizing the connection between the Radon transform and the Fourier transform, we interpret the kernel regime's inductive bias as minimizing a spectral seminorm that penalizes high-frequency components, in a manner dependent on the activation function. Finally, in the adaptive regime, we demonstrate the existence of local dynamical attractors that facilitate the formation of clusters of hyperplanes where the input to a neuron's activation function is zero, yielding alignment between many neurons' response functions. We confirm these theoretical results with simulations. All together, our work provides a deeper understanding of the mechanisms underlying the generalization capabilities of overparameterized neural networks and its relation with the implicit bias, offering potential pathways for designing more efficient and robust models.

Shallow Univariate ReLu Networks as Splines: Initialization, Loss Surface, Hessian, & Gradient Flow Dynamics

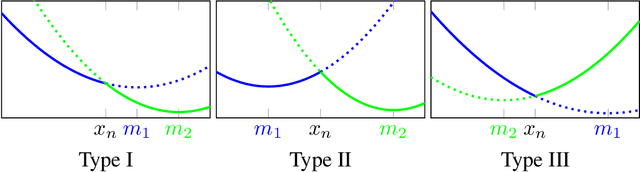
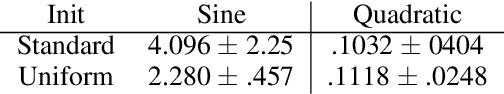
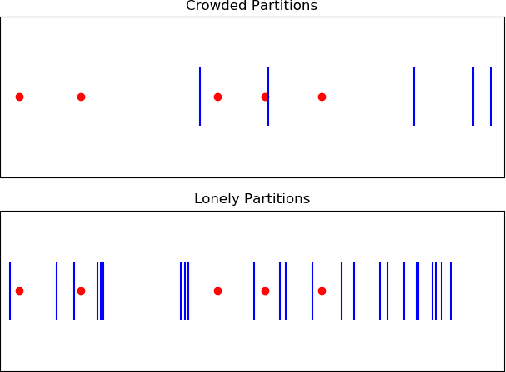
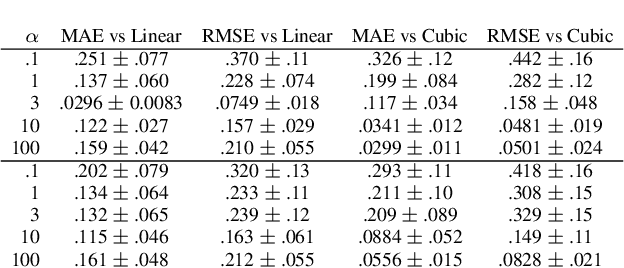
Understanding the learning dynamics and inductive bias of neural networks (NNs) is hindered by the opacity of the relationship between NN parameters and the function represented. We propose reparametrizing ReLU NNs as continuous piecewise linear splines. Using this spline lens, we study learning dynamics in shallow univariate ReLU NNs, finding unexpected insights and explanations for several perplexing phenomena. We develop a surprisingly simple and transparent view of the structure of the loss surface, including its critical and fixed points, Hessian, and Hessian spectrum. We also show that standard weight initializations yield very flat functions, and that this flatness, together with overparametrization and the initial weight scale, is responsible for the strength and type of implicit regularization, consistent with recent work arXiv:1906.05827. Our implicit regularization results are complementary to recent work arXiv:1906.07842, done independently, which showed that initialization scale critically controls implicit regularization via a kernel-based argument. Our spline-based approach reproduces their key implicit regularization results but in a far more intuitive and transparent manner. Going forward, our spline-based approach is likely to extend naturally to the multivariate and deep settings, and will play a foundational role in efforts to understand neural networks. Videos of learning dynamics using a spline-based visualization are available at http://shorturl.at/tFWZ2.