Geometry-Based Data Generation
Paper and Code
Sep 06, 2018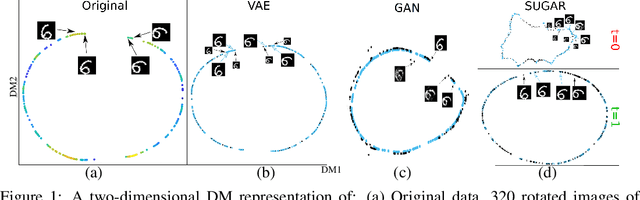

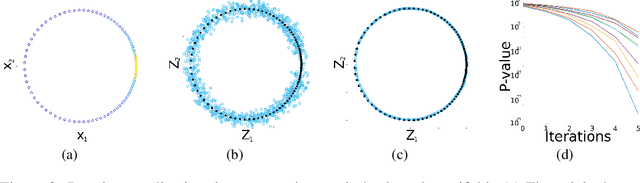
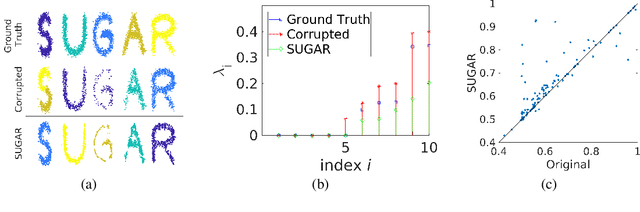
Many generative models attempt to replicate the density of their input data. However, this approach is often undesirable, since data density is highly affected by sampling biases, noise, and artifacts. We propose a method called SUGAR (Synthesis Using Geometrically Aligned Random-walks) that uses a diffusion process to learn a manifold geometry from the data. Then, it generates new points evenly along the manifold by pulling randomly generated points into its intrinsic structure using a diffusion kernel. SUGAR equalizes the density along the manifold by selectively generating points in sparse areas of the manifold. We demonstrate how the approach corrects sampling biases and artifacts, while also revealing intrinsic patterns (e.g. progression) and relations in the data. The method is applicable for correcting missing data, finding hypothetical data points, and learning relationships between data features.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge