SystemMatch: optimizing preclinical drug models to human clinical outcomes via generative latent-space matching

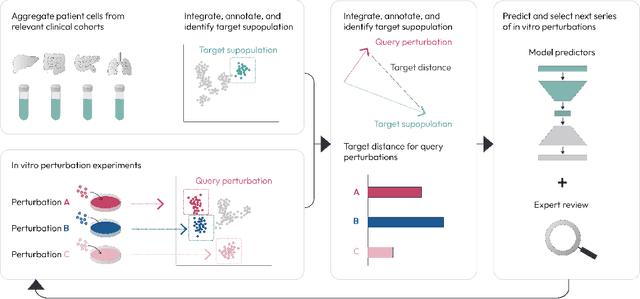
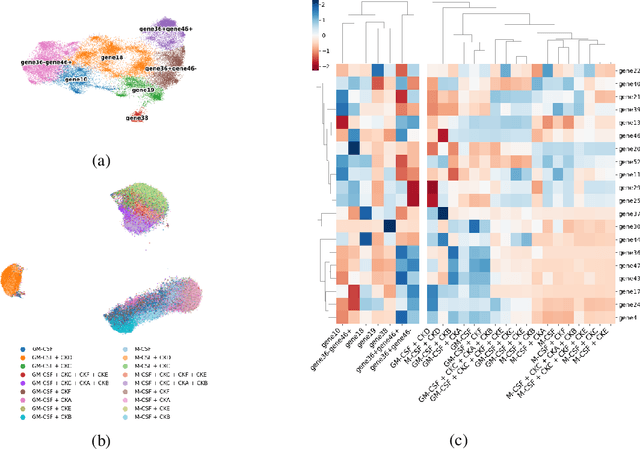
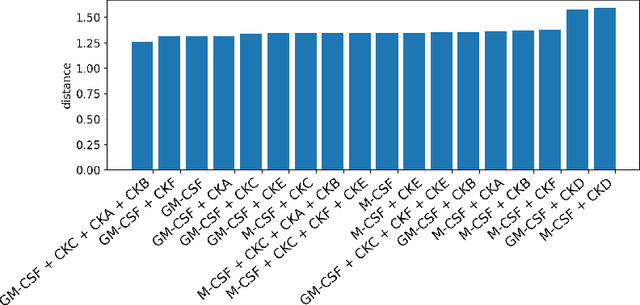
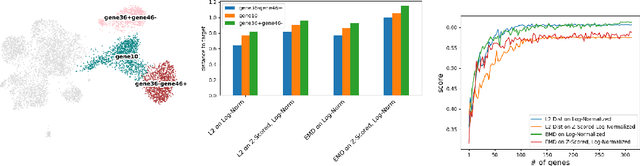
Translating the relevance of preclinical models ($\textit{in vitro}$, animal models, or organoids) to their relevance in humans presents an important challenge during drug development. The rising abundance of single-cell genomic data from human tumors and tissue offers a new opportunity to optimize model systems by their similarity to targeted human cell types in disease. In this work, we introduce SystemMatch to assess the fit of preclinical model systems to an $\textit{in sapiens}$ target population and to recommend experimental changes to further optimize these systems. We demonstrate this through an application to developing $\textit{in vitro}$ systems to model human tumor-derived suppressive macrophages. We show with held-out $\textit{in vivo}$ controls that our pipeline successfully ranks macrophage subpopulations by their biological similarity to the target population, and apply this analysis to rank a series of 18 $\textit{in vitro}$ macrophage systems perturbed with a variety of cytokine stimulations. We extend this analysis to predict the behavior of 66 $\textit{in silico}$ model systems generated using a perturbational autoencoder and apply a $k$-medoids approach to recommend a subset of these model systems for further experimental development in order to fully explore the space of possible perturbations. Through this use case, we demonstrate a novel approach to model system development to generate a system more similar to human biology.

Visualizing the PHATE of Neural Networks

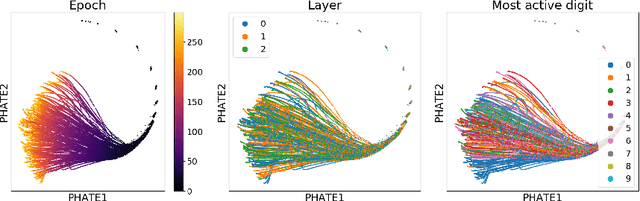
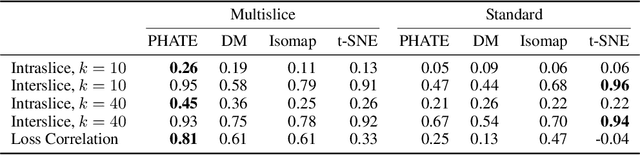
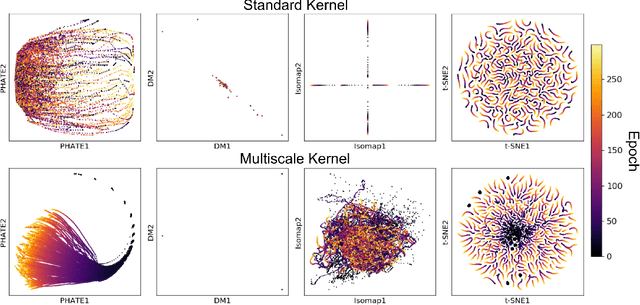
Understanding why and how certain neural networks outperform others is key to guiding future development of network architectures and optimization methods. To this end, we introduce a novel visualization algorithm that reveals the internal geometry of such networks: Multislice PHATE (M-PHATE), the first method designed explicitly to visualize how a neural network's hidden representations of data evolve throughout the course of training. We demonstrate that our visualization provides intuitive, detailed summaries of the learning dynamics beyond simple global measures (i.e., validation loss and accuracy), without the need to access validation data. Furthermore, M-PHATE better captures both the dynamics and community structure of the hidden units as compared to visualization based on standard dimensionality reduction methods (e.g., ISOMAP, t-SNE). We demonstrate M-PHATE with two vignettes: continual learning and generalization. In the former, the M-PHATE visualizations display the mechanism of "catastrophic forgetting" which is a major challenge for learning in task-switching contexts. In the latter, our visualizations reveal how increased heterogeneity among hidden units correlates with improved generalization performance. An implementation of M-PHATE, along with scripts to reproduce the figures in this paper, is available at https://github.com/scottgigante/M-PHATE.

Compressed Diffusion

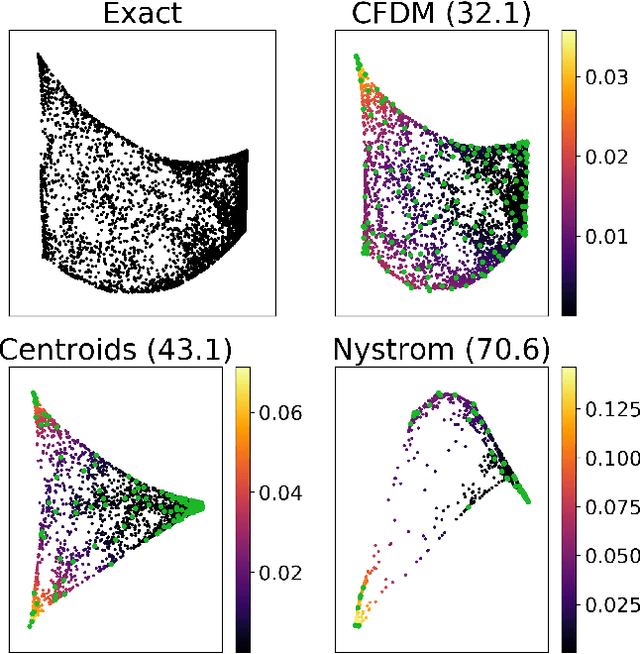
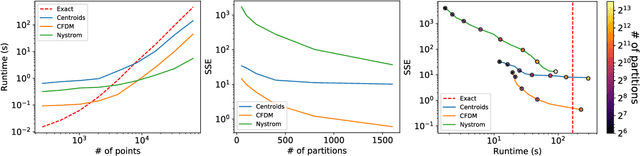
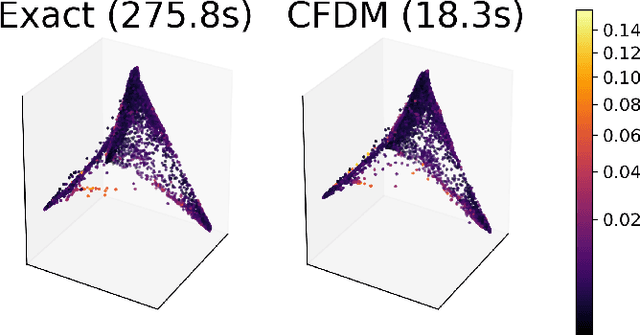
Diffusion maps are a commonly used kernel-based method for manifold learning, which can reveal intrinsic structures in data and embed them in low dimensions. However, as with most kernel methods, its implementation requires a heavy computational load, reaching up to cubic complexity in the number of data points. This limits its usability in modern data analysis. Here, we present a new approach to computing the diffusion geometry, and related embeddings, from a compressed diffusion process between data regions rather than data points. Our construction is based on an adaptation of the previously proposed measure-based (MGC) kernel that robustly captures the local geometry around data points. We use this MGC kernel to efficiently compress diffusion relations from pointwise to data region resolution. Finally, a spectral embedding of the data regions provides coordinates that are used to interpolate and approximate the pointwise diffusion map embedding of data. We analyze theoretical connections between our construction and the original diffusion geometry of diffusion maps, and demonstrate the utility of our method in analyzing big datasets, where it outperforms competing approaches.

Modeling Dynamics of Biological Systems with Deep Generative Neural Networks

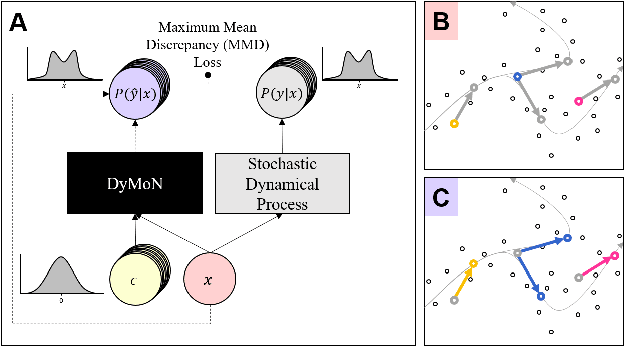
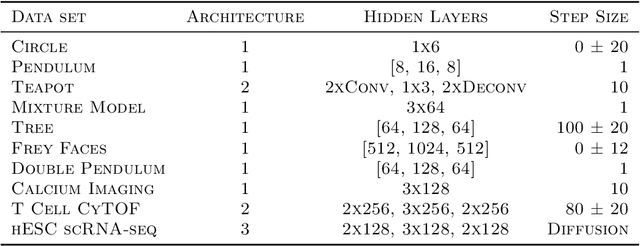
Biological data often contains measurements of dynamic entities such as cells or organisms in various states of progression. However, biological systems are notoriously difficult to describe analytically due to their many interacting components, and in many cases, the technical challenge of taking longitudinal measurements. This leads to difficulties in studying the features of the dynamics, for examples the drivers of the transition. To address this problem, we present a deep neural network framework we call Dynamics Modeling Network or DyMoN. DyMoN is a neural network framework trained as a deep generative Markov model whose next state is a probability distribution based on the current state. DyMoN is well-suited to the idiosyncrasies of biological data, including noise, sparsity, and the lack of longitudinal measurements in many types of systems. Thus, DyMoN can be trained using probability distributions derived from the data in any way, such as trajectories derived via dimensionality reduction methods, and does not require longitudinal measurements. We show the advantage of learning deep models over shallow models such as Kalman filters and hidden Markov models that do not learn representations of the data, both in terms of learning embeddings of the data and also in terms training efficiency, accuracy and ability to multitask. We perform three case studies of applying DyMoN to different types of biological systems and extracting features of the dynamics in each case by examining the learned model.