Variance Minimization in the Wasserstein Space for Invariant Causal Prediction

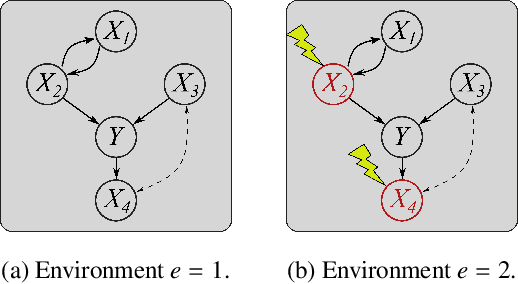
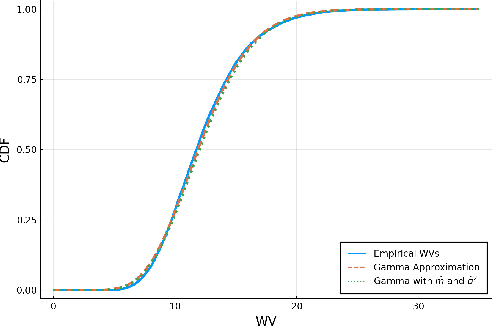
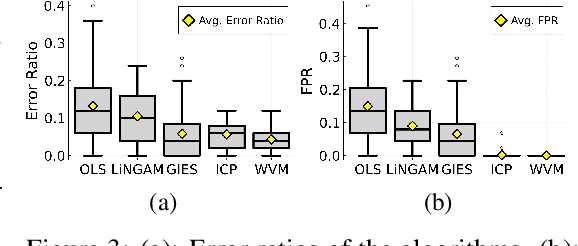
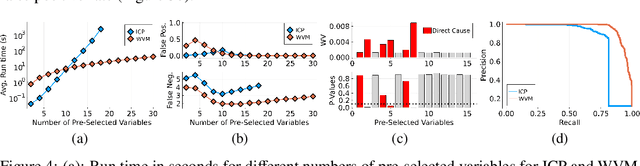
Selecting powerful predictors for an outcome is a cornerstone task for machine learning. However, some types of questions can only be answered by identifying the predictors that causally affect the outcome. A recent approach to this causal inference problem leverages the invariance property of a causal mechanism across differing experimental environments (Peters et al., 2016; Heinze-Deml et al., 2018). This method, invariant causal prediction (ICP), has a substantial computational defect -- the runtime scales exponentially with the number of possible causal variables. In this work, we show that the approach taken in ICP may be reformulated as a series of nonparametric tests that scales linearly in the number of predictors. Each of these tests relies on the minimization of a novel loss function -- the Wasserstein variance -- that is derived from tools in optimal transport theory and is used to quantify distributional variability across environments. We prove under mild assumptions that our method is able to recover the set of identifiable direct causes, and we demonstrate in our experiments that it is competitive with other benchmark causal discovery algorithms.

Modeling Dynamics of Biological Systems with Deep Generative Neural Networks

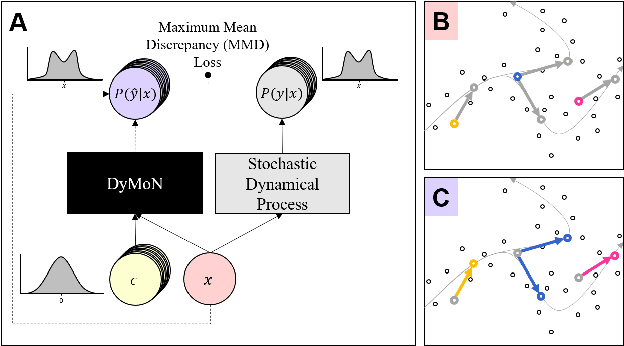
Biological data often contains measurements of dynamic entities such as cells or organisms in various states of progression. However, biological systems are notoriously difficult to describe analytically due to their many interacting components, and in many cases, the technical challenge of taking longitudinal measurements. This leads to difficulties in studying the features of the dynamics, for examples the drivers of the transition. To address this problem, we present a deep neural network framework we call Dynamics Modeling Network or DyMoN. DyMoN is a neural network framework trained as a deep generative Markov model whose next state is a probability distribution based on the current state. DyMoN is well-suited to the idiosyncrasies of biological data, including noise, sparsity, and the lack of longitudinal measurements in many types of systems. Thus, DyMoN can be trained using probability distributions derived from the data in any way, such as trajectories derived via dimensionality reduction methods, and does not require longitudinal measurements. We show the advantage of learning deep models over shallow models such as Kalman filters and hidden Markov models that do not learn representations of the data, both in terms of learning embeddings of the data and also in terms training efficiency, accuracy and ability to multitask. We perform three case studies of applying DyMoN to different types of biological systems and extracting features of the dynamics in each case by examining the learned model.