Incorporating Taylor Series and Recursive Structure in Neural Networks for Time Series Prediction

Time series analysis is relevant in various disciplines such as physics, biology, chemistry, and finance. In this paper, we present a novel neural network architecture that integrates elements from ResNet structures, while introducing the innovative incorporation of the Taylor series framework. This approach demonstrates notable enhancements in test accuracy across many of the baseline datasets investigated. Furthermore, we extend our method to incorporate a recursive step, which leads to even further improvements in test accuracy. Our findings underscore the potential of our proposed model to significantly advance time series analysis methodologies, offering promising avenues for future research and application.

Exploring higher-order neural network node interactions with total correlation

In domains such as ecological systems, collaborations, and the human brain the variables interact in complex ways. Yet accurately characterizing higher-order variable interactions (HOIs) is a difficult problem that is further exacerbated when the HOIs change across the data. To solve this problem we propose a new method called Local Correlation Explanation (CorEx) to capture HOIs at a local scale by first clustering data points based on their proximity on the data manifold. We then use a multivariate version of the mutual information called the total correlation, to construct a latent factor representation of the data within each cluster to learn the local HOIs. We use Local CorEx to explore HOIs in synthetic and real world data to extract hidden insights about the data structure. Lastly, we demonstrate Local CorEx's suitability to explore and interpret the inner workings of trained neural networks.

Compressed Diffusion

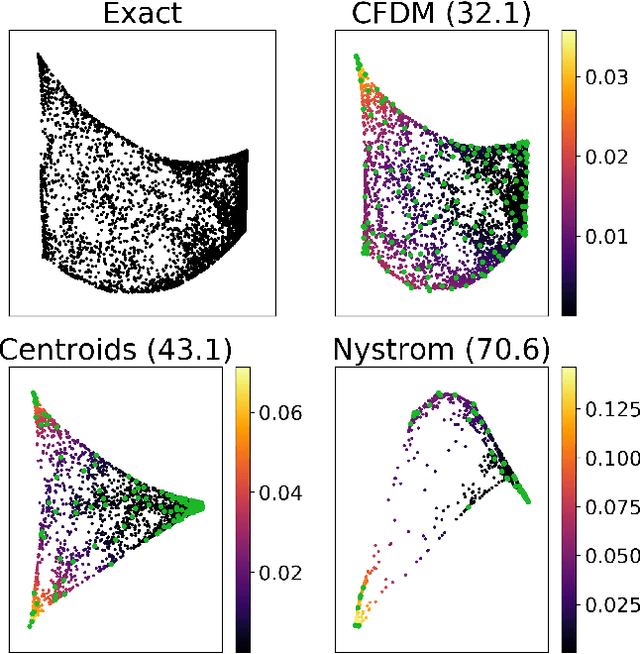
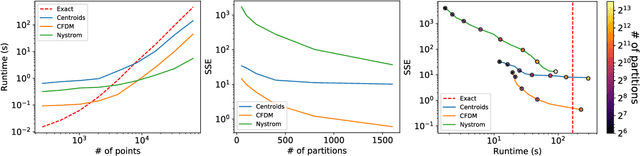
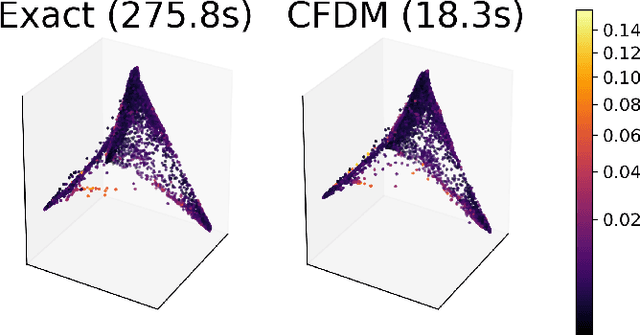
Diffusion maps are a commonly used kernel-based method for manifold learning, which can reveal intrinsic structures in data and embed them in low dimensions. However, as with most kernel methods, its implementation requires a heavy computational load, reaching up to cubic complexity in the number of data points. This limits its usability in modern data analysis. Here, we present a new approach to computing the diffusion geometry, and related embeddings, from a compressed diffusion process between data regions rather than data points. Our construction is based on an adaptation of the previously proposed measure-based (MGC) kernel that robustly captures the local geometry around data points. We use this MGC kernel to efficiently compress diffusion relations from pointwise to data region resolution. Finally, a spectral embedding of the data regions provides coordinates that are used to interpolate and approximate the pointwise diffusion map embedding of data. We analyze theoretical connections between our construction and the original diffusion geometry of diffusion maps, and demonstrate the utility of our method in analyzing big datasets, where it outperforms competing approaches.

Modeling Dynamics of Biological Systems with Deep Generative Neural Networks

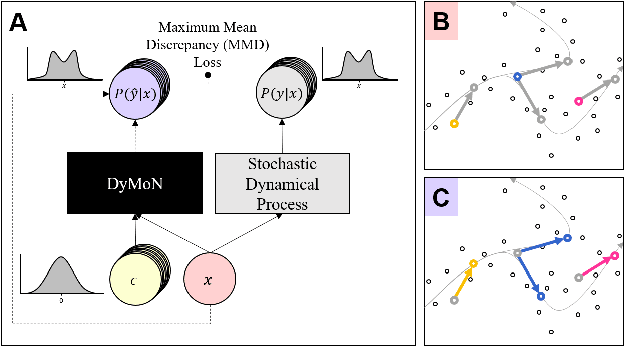
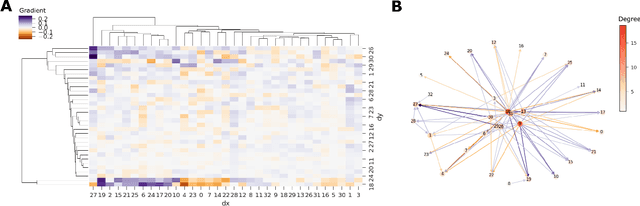
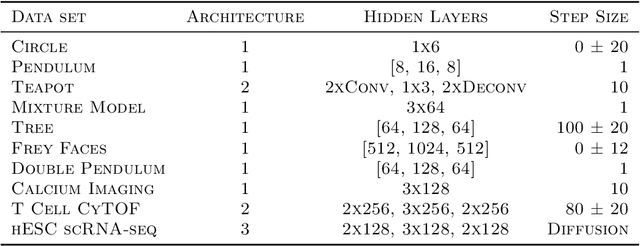
Biological data often contains measurements of dynamic entities such as cells or organisms in various states of progression. However, biological systems are notoriously difficult to describe analytically due to their many interacting components, and in many cases, the technical challenge of taking longitudinal measurements. This leads to difficulties in studying the features of the dynamics, for examples the drivers of the transition. To address this problem, we present a deep neural network framework we call Dynamics Modeling Network or DyMoN. DyMoN is a neural network framework trained as a deep generative Markov model whose next state is a probability distribution based on the current state. DyMoN is well-suited to the idiosyncrasies of biological data, including noise, sparsity, and the lack of longitudinal measurements in many types of systems. Thus, DyMoN can be trained using probability distributions derived from the data in any way, such as trajectories derived via dimensionality reduction methods, and does not require longitudinal measurements. We show the advantage of learning deep models over shallow models such as Kalman filters and hidden Markov models that do not learn representations of the data, both in terms of learning embeddings of the data and also in terms training efficiency, accuracy and ability to multitask. We perform three case studies of applying DyMoN to different types of biological systems and extracting features of the dynamics in each case by examining the learned model.