Variance Minimization in the Wasserstein Space for Invariant Causal Prediction

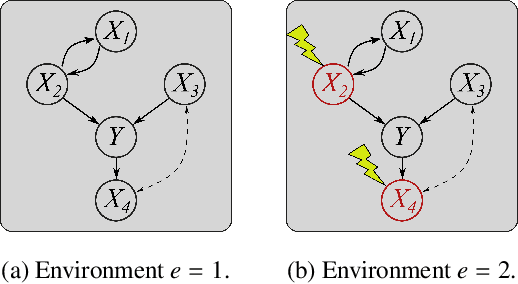
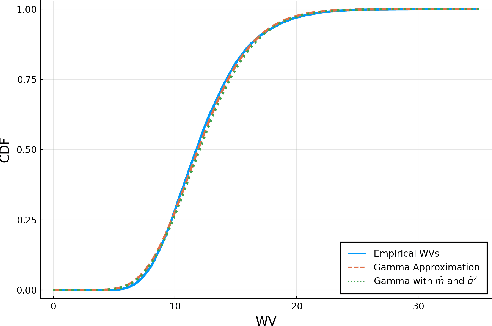
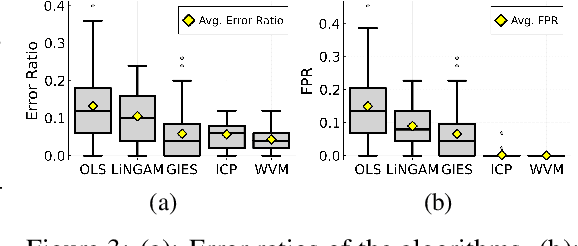
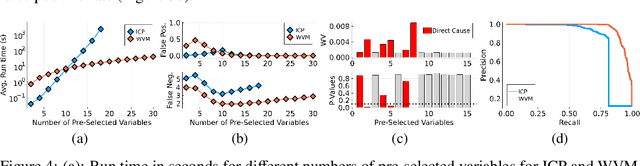
Selecting powerful predictors for an outcome is a cornerstone task for machine learning. However, some types of questions can only be answered by identifying the predictors that causally affect the outcome. A recent approach to this causal inference problem leverages the invariance property of a causal mechanism across differing experimental environments (Peters et al., 2016; Heinze-Deml et al., 2018). This method, invariant causal prediction (ICP), has a substantial computational defect -- the runtime scales exponentially with the number of possible causal variables. In this work, we show that the approach taken in ICP may be reformulated as a series of nonparametric tests that scales linearly in the number of predictors. Each of these tests relies on the minimization of a novel loss function -- the Wasserstein variance -- that is derived from tools in optimal transport theory and is used to quantify distributional variability across environments. We prove under mild assumptions that our method is able to recover the set of identifiable direct causes, and we demonstrate in our experiments that it is competitive with other benchmark causal discovery algorithms.

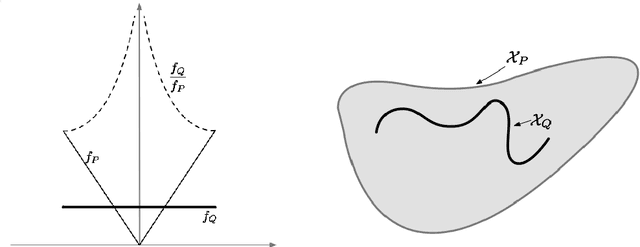
Marginal Singularity, and the Benefits of Labels in Covariate-Shift

We present new minimax results that concisely capture the relative benefits of source and target labeled data, under covariate-shift. Namely, we show that the benefits of target labels are controlled by a transfer-exponent $\gamma$ that encodes how singular Q is locally w.r.t. P, and interestingly allows situations where transfer did not seem possible under previous insights. In fact, our new minimax analysis - in terms of $\gamma$ - reveals a continuum of regimes ranging from situations where target labels have little benefit, to regimes where target labels dramatically improve classification. We then show that a recently proposed semi-supervised procedure can be extended to adapt to unknown $\gamma$, and therefore requests labels only when beneficial, while achieving minimax transfer rates.