Marginal Singularity, and the Benefits of Labels in Covariate-Shift
Paper and Code
Jun 04, 2018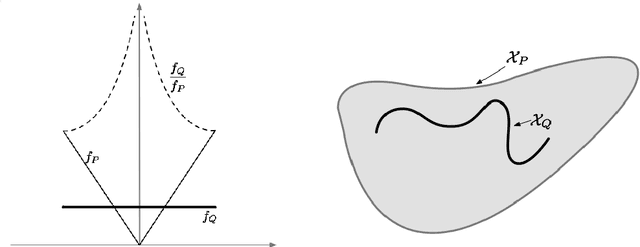
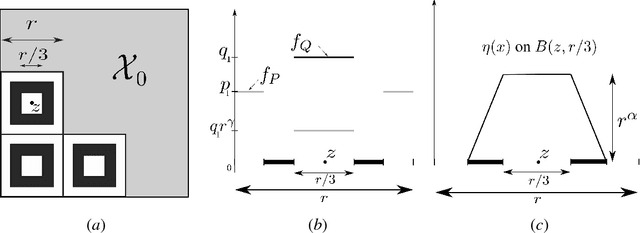
We present new minimax results that concisely capture the relative benefits of source and target labeled data, under covariate-shift. Namely, we show that the benefits of target labels are controlled by a transfer-exponent $\gamma$ that encodes how singular Q is locally w.r.t. P, and interestingly allows situations where transfer did not seem possible under previous insights. In fact, our new minimax analysis - in terms of $\gamma$ - reveals a continuum of regimes ranging from situations where target labels have little benefit, to regimes where target labels dramatically improve classification. We then show that a recently proposed semi-supervised procedure can be extended to adapt to unknown $\gamma$, and therefore requests labels only when beneficial, while achieving minimax transfer rates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge