Probabilistic Decomposed Linear Dynamical Systems for Robust Discovery of Latent Neural Dynamics

Time-varying linear state-space models are powerful tools for obtaining mathematically interpretable representations of neural signals. For example, switching and decomposed models describe complex systems using latent variables that evolve according to simple locally linear dynamics. However, existing methods for latent variable estimation are not robust to dynamical noise and system nonlinearity due to noise-sensitive inference procedures and limited model formulations. This can lead to inconsistent results on signals with similar dynamics, limiting the model's ability to provide scientific insight. In this work, we address these limitations and propose a probabilistic approach to latent variable estimation in decomposed models that improves robustness against dynamical noise. Additionally, we introduce an extended latent dynamics model to improve robustness against system nonlinearities. We evaluate our approach on several synthetic dynamical systems, including an empirically-derived brain-computer interface experiment, and demonstrate more accurate latent variable inference in nonlinear systems with diverse noise conditions. Furthermore, we apply our method to a real-world clinical neurophysiology dataset, illustrating the ability to identify interpretable and coherent structure where previous models cannot.

Unsupervised discovery of the shared and private geometry in multi-view data

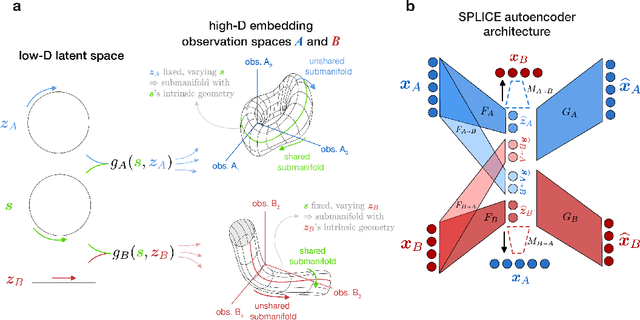
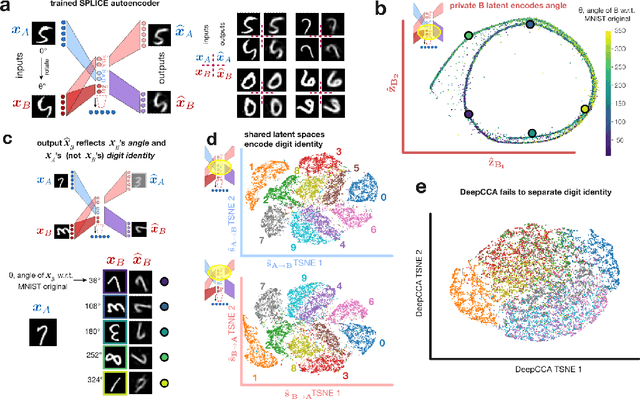
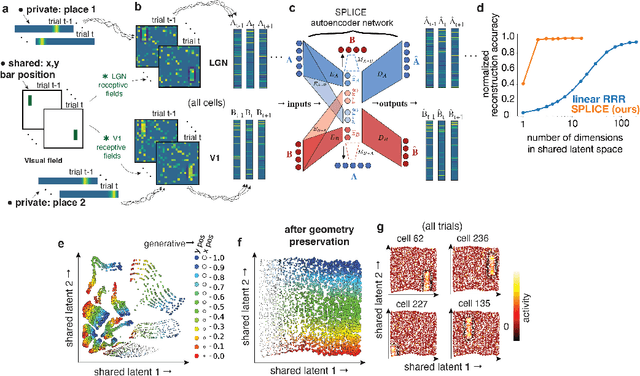
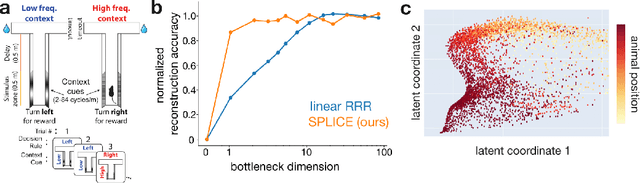
Modern applications often leverage multiple views of a subject of study. Within neuroscience, there is growing interest in large-scale simultaneous recordings across multiple brain regions. Understanding the relationship between views (e.g., the neural activity in each region recorded) can reveal fundamental principles about the characteristics of each representation and about the system. However, existing methods to characterize such relationships either lack the expressivity required to capture complex nonlinearities, describe only sources of variance that are shared between views, or discard geometric information that is crucial to interpreting the data. Here, we develop a nonlinear neural network-based method that, given paired samples of high-dimensional views, disentangles low-dimensional shared and private latent variables underlying these views while preserving intrinsic data geometry. Across multiple simulated and real datasets, we demonstrate that our method outperforms competing methods. Using simulated populations of lateral geniculate nucleus (LGN) and V1 neurons we demonstrate our model's ability to discover interpretable shared and private structure across different noise conditions. On a dataset of unrotated and corresponding but randomly rotated MNIST digits, we recover private latents for the rotated view that encode rotation angle regardless of digit class, and places the angle representation on a 1-d manifold, while shared latents encode digit class but not rotation angle. Applying our method to simultaneous Neuropixels recordings of hippocampus and prefrontal cortex while mice run on a linear track, we discover a low-dimensional shared latent space that encodes the animal's position. We propose our approach as a general-purpose method for finding succinct and interpretable descriptions of paired data sets in terms of disentangled shared and private latent variables.

CrEIMBO: Cross Ensemble Interactions in Multi-view Brain Observations

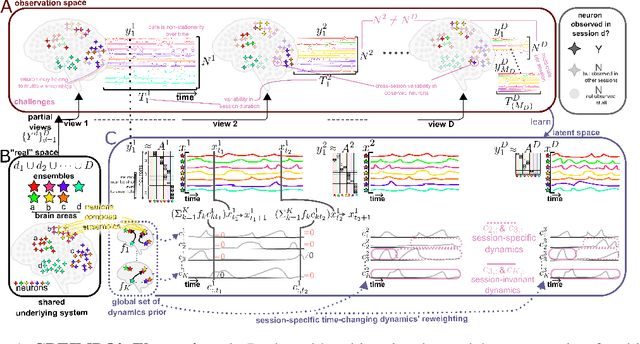
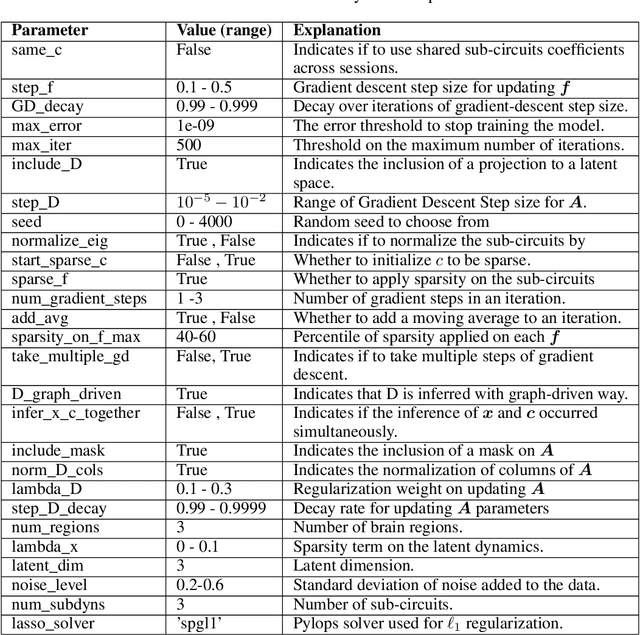
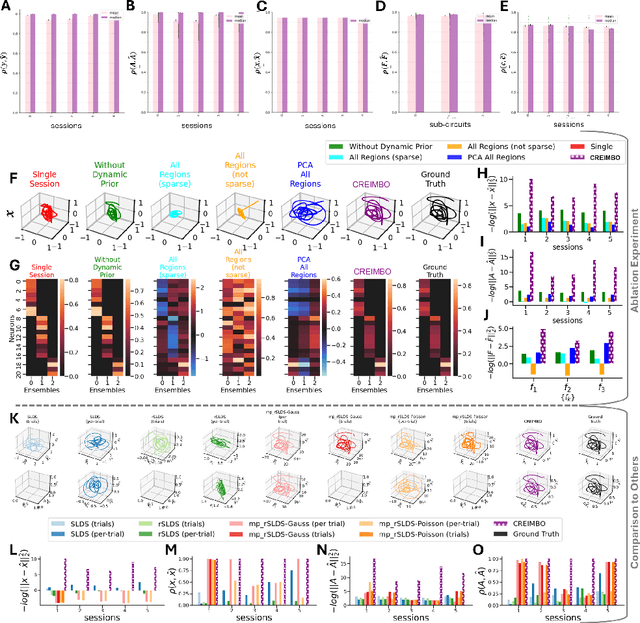
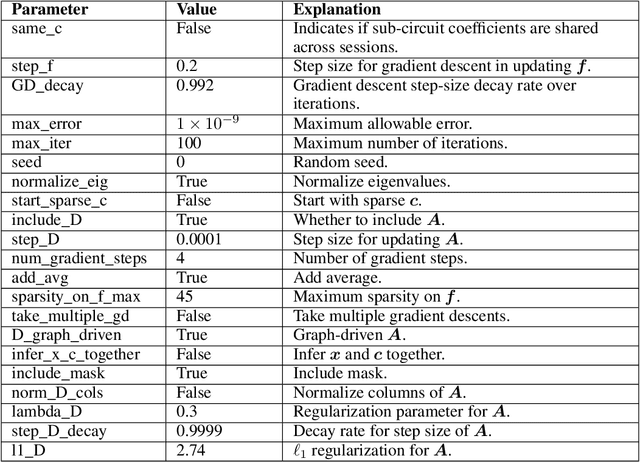
Modern recordings of neural activity provide diverse observations of neurons across brain areas, behavioral conditions, and subjects -- thus presenting an exciting opportunity to reveal the fundamentals of brain-wide dynamics underlying cognitive function. Current methods, however, often fail to fully harness the richness of such data as they either provide an uninterpretable representation (e.g., via "black box" deep networks) or over-simplify the model (e.g., assume stationary dynamics or analyze each session independently). Here, instead of regarding asynchronous recordings that lack alignment in neural identity or brain areas as a limitation, we exploit these diverse views of the same brain system to learn a unified model of brain dynamics. We assume that brain observations stem from the joint activity of a set of functional neural ensembles (groups of co-active neurons) that are similar in functionality across recordings, and propose to discover the ensemble and their non-stationary dynamical interactions in a new model we term CrEIMBO (Cross-Ensemble Interactions in Multi-view Brain Observations). CrEIMBO identifies the composition of the per-session neural ensembles through graph-driven dictionary learning and models the ensemble dynamics as a latent sparse time-varying decomposition of global sub-circuits, thereby capturing non-stationary dynamics. CrEIMBO identifies multiple co-active sub-circuits while maintaining representation interpretability due to sharing sub-circuits across sessions. CrEIMBO distinguishes session-specific from global (session-invariant) computations by exploring when distinct sub-circuits are active. We demonstrate CrEIMBO's ability to recover ground truth components in synthetic data and uncover meaningful brain dynamics, capturing cross-subject and inter- and intra-area variability, in high-density electrode recordings of humans performing a memory task.

realSEUDO for real-time calcium imaging analysis

Closed-loop neuroscience experimentation, where recorded neural activity is used to modify the experiment on-the-fly, is critical for deducing causal connections and optimizing experimental time. A critical step in creating a closed-loop experiment is real-time inference of neural activity from streaming recordings. One challenging modality for real-time processing is multi-photon calcium imaging (CI). CI enables the recording of activity in large populations of neurons however, often requires batch processing of the video data to extract single-neuron activity from the fluorescence videos. We use the recently proposed robust time-trace estimator-Sparse Emulation of Unused Dictionary Objects (SEUDO) algorithm-as a basis for a new on-line processing algorithm that simultaneously identifies neurons in the fluorescence video and infers their time traces in a way that is robust to as-yet unidentified neurons. To achieve real-time SEUDO (realSEUDO), we optimize the core estimator via both algorithmic improvements and an fast C-based implementation, and create a new cell finding loop to enable realSEUDO to also identify new cells. We demonstrate comparable performance to offline algorithms (e.g., CNMF), and improved performance over the current on-line approach (OnACID) at speeds of 120 Hz on average.

SiBBlInGS: Similarity-driven Building-Block Inference using Graphs across States

Interpretable methods for extracting meaningful building blocks (BBs) underlying multi-dimensional time series are vital for discovering valuable insights in complex systems. Existing techniques, however, encounter limitations that restrict their applicability to real-world systems, like reliance on orthogonality assumptions, inadequate incorporation of inter- and intra-state variability, and incapability to handle sessions of varying duration. Here, we present a framework for Similarity-driven Building Block Inference using Graphs across States (SiBBlInGS). SiBBlInGS employs a graph-based dictionary learning approach for BB discovery, simultaneously considers both inter- and intra-state relationships in the data, can extract non-orthogonal components, and allows for variations in session counts and duration across states. Additionally, SiBBlInGS allows for cross-state variations in BB structure and per-trial temporal variability, can identify state-specific vs state-invariant BBs, and offers both supervised and data-driven approaches for controlling the level of BB similarity between states. We demonstrate SiBBlInGS on synthetic and real-world data to highlight its ability to provide insights into the underlying mechanisms of complex phenomena and its applicability to data in various fields.

Multi-Lingual DALL-E Storytime

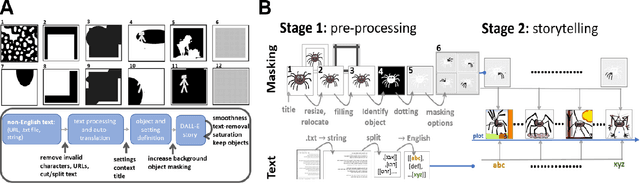
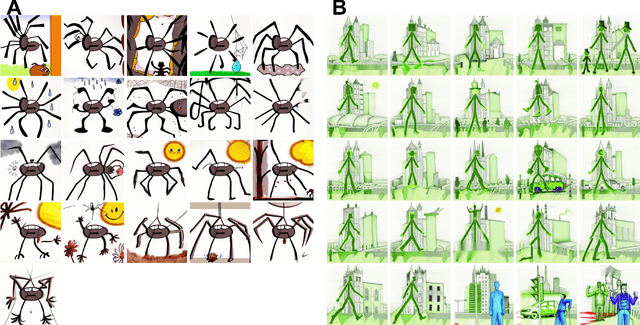
While recent advancements in artificial intelligence (AI) language models demonstrate cutting-edge performance when working with English texts, equivalent models do not exist in other languages or do not reach the same performance level. This undesired effect of AI advancements increases the gap between access to new technology from different populations across the world. This unsought bias mainly discriminates against individuals whose English skills are less developed, e.g., non-English speakers children. Following significant advancements in AI research in recent years, OpenAI has recently presented DALL-E: a powerful tool for creating images based on English text prompts. While DALL-E is a promising tool for many applications, its decreased performance when given input in a different language, limits its audience and deepens the gap between populations. An additional limitation of the current DALL-E model is that it only allows for the creation of a few images in response to a given input prompt, rather than a series of consecutive coherent frames that tell a story or describe a process that changes over time. Here, we present an easy-to-use automatic DALL-E storytelling framework that leverages the existing DALL-E model to enable fast and coherent visualizations of non-English songs and stories, pushing the limit of the one-step-at-a-time option DALL-E currently offers. We show that our framework is able to effectively visualize stories from non-English texts and portray the changes in the plot over time. It is also able to create a narrative and maintain interpretable changes in the description across frames. Additionally, our framework offers users the ability to specify constraints on the story elements, such as a specific location or context, and to maintain a consistent style throughout the visualization.

Decomposed Linear Dynamical Systems (dLDS) for learning the latent components of neural dynamics

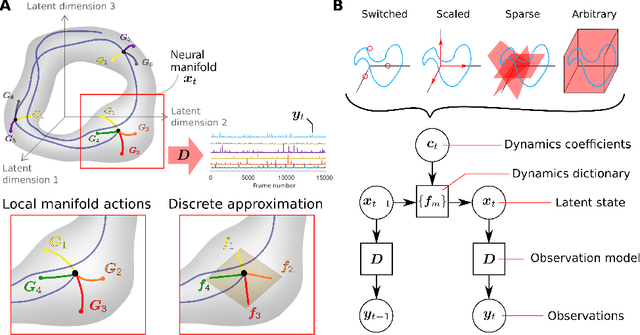
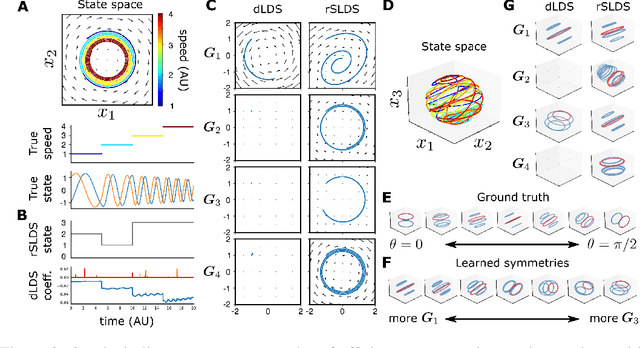
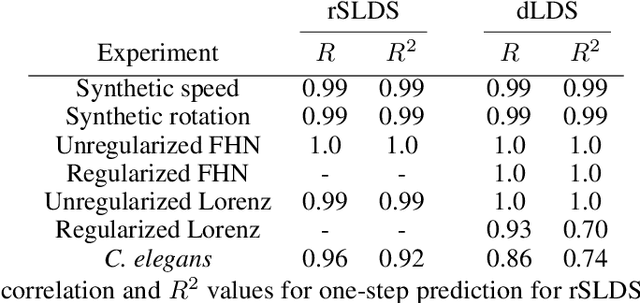
Learning interpretable representations of neural dynamics at a population level is a crucial first step to understanding how neural activity relates to perception and behavior. Models of neural dynamics often focus on either low-dimensional projections of neural activity, or on learning dynamical systems that explicitly relate to the neural state over time. We discuss how these two approaches are interrelated by considering dynamical systems as representative of flows on a low-dimensional manifold. Building on this concept, we propose a new decomposed dynamical system model that represents complex non-stationary and nonlinear dynamics of time-series data as a sparse combination of simpler, more interpretable components. The decomposed nature of the dynamics generalizes over previous switched approaches and enables modeling of overlapping and non-stationary drifts in the dynamics. We further present a dictionary learning-driven approach to model fitting, where we leverage recent results in tracking sparse vectors over time. We demonstrate that our model can learn efficient representations and smooth transitions between dynamical modes in both continuous-time and discrete-time examples. We show results on low-dimensional linear and nonlinear attractors to demonstrate that our decomposed dynamical systems model can well approximate nonlinear dynamics. Additionally, we apply our model to C. elegans data, illustrating a diversity of dynamics that is obscured when classified into discrete states.

Data Processing of Functional Optical Microscopy for Neuroscience

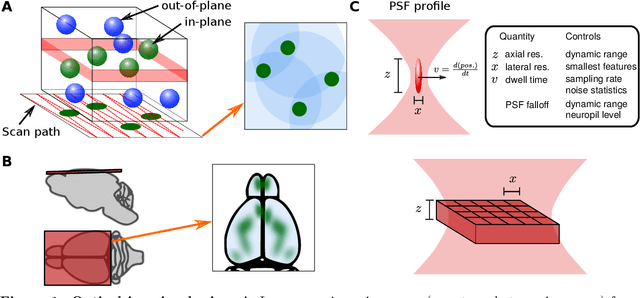
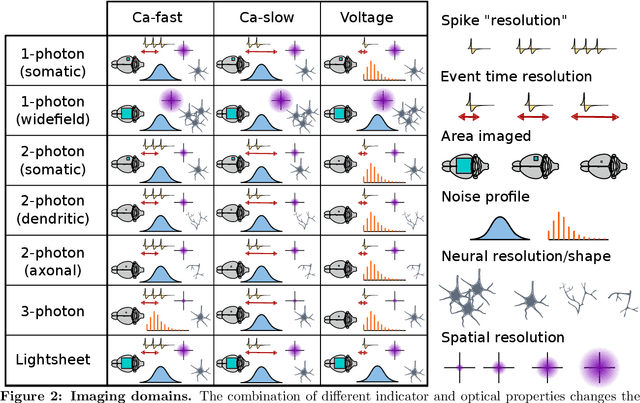
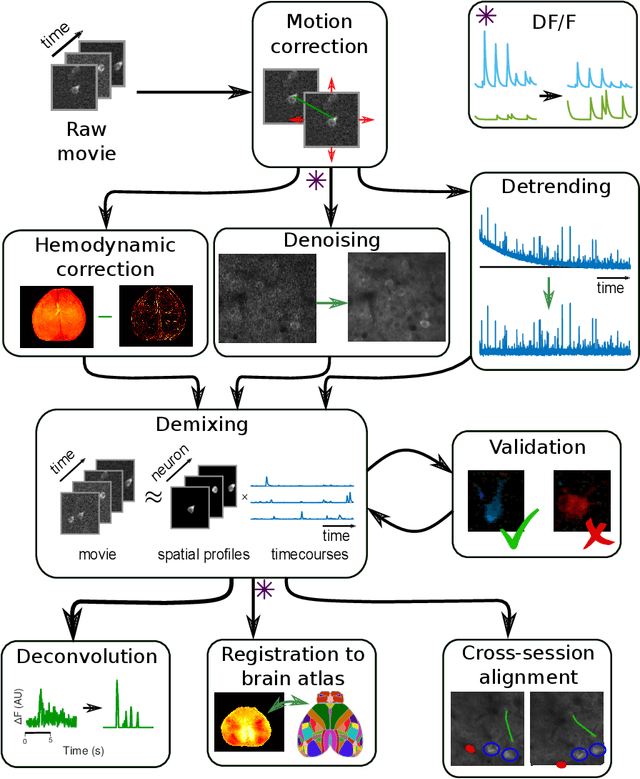
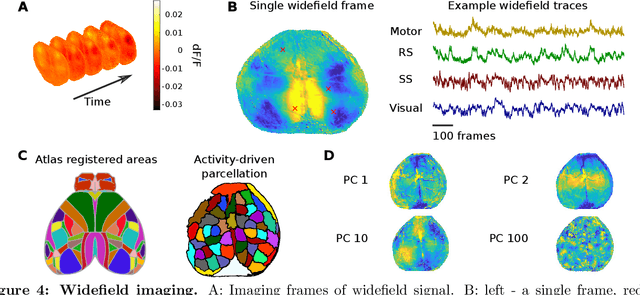
Functional optical imaging in neuroscience is rapidly growing with the development of new optical systems and fluorescence indicators. To realize the potential of these massive spatiotemporal datasets for relating neuronal activity to behavior and stimuli and uncovering local circuits in the brain, accurate automated processing is increasingly essential. In this review, we cover recent computational developments in the full data processing pipeline of functional optical microscopy for neuroscience data and discuss ongoing and emerging challenges.

Visualizing the PHATE of Neural Networks

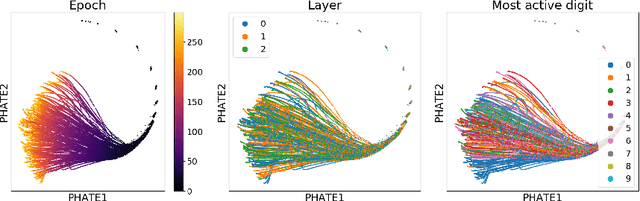
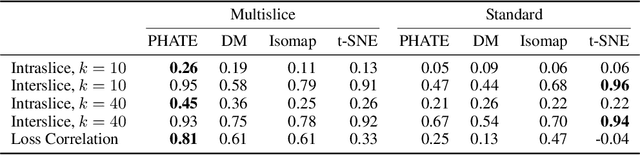
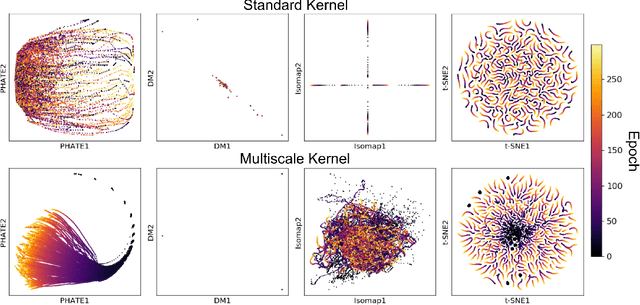
Understanding why and how certain neural networks outperform others is key to guiding future development of network architectures and optimization methods. To this end, we introduce a novel visualization algorithm that reveals the internal geometry of such networks: Multislice PHATE (M-PHATE), the first method designed explicitly to visualize how a neural network's hidden representations of data evolve throughout the course of training. We demonstrate that our visualization provides intuitive, detailed summaries of the learning dynamics beyond simple global measures (i.e., validation loss and accuracy), without the need to access validation data. Furthermore, M-PHATE better captures both the dynamics and community structure of the hidden units as compared to visualization based on standard dimensionality reduction methods (e.g., ISOMAP, t-SNE). We demonstrate M-PHATE with two vignettes: continual learning and generalization. In the former, the M-PHATE visualizations display the mechanism of "catastrophic forgetting" which is a major challenge for learning in task-switching contexts. In the latter, our visualizations reveal how increased heterogeneity among hidden units correlates with improved generalization performance. An implementation of M-PHATE, along with scripts to reproduce the figures in this paper, is available at https://github.com/scottgigante/M-PHATE.

Interpreting Deep Learning: The Machine Learning Rorschach Test?

Theoretical understanding of deep learning is one of the most important tasks facing the statistics and machine learning communities. While deep neural networks (DNNs) originated as engineering methods and models of biological networks in neuroscience and psychology, they have quickly become a centerpiece of the machine learning toolbox. Unfortunately, DNN adoption powered by recent successes combined with the open-source nature of the machine learning community, has outpaced our theoretical understanding. We cannot reliably identify when and why DNNs will make mistakes. In some applications like text translation these mistakes may be comical and provide for fun fodder in research talks, a single error can be very costly in tasks like medical imaging. As we utilize DNNs in increasingly sensitive applications, a better understanding of their properties is thus imperative. Recent advances in DNN theory are numerous and include many different sources of intuition, such as learning theory, sparse signal analysis, physics, chemistry, and psychology. An interesting pattern begins to emerge in the breadth of possible interpretations. The seemingly limitless approaches are mostly constrained by the lens with which the mathematical operations are viewed. Ultimately, the interpretation of DNNs appears to mimic a type of Rorschach test --- a psychological test wherein subjects interpret a series of seemingly ambiguous ink-blots. Validation for DNN theory requires a convergence of the literature. We must distinguish between universal results that are invariant to the analysis perspective and those that are specific to a particular network configuration. Simultaneously we must deal with the fact that many standard statistical tools for quantifying generalization or empirically assessing important network features are difficult to apply to DNNs.