Probabilistic Decomposed Linear Dynamical Systems for Robust Discovery of Latent Neural Dynamics

Time-varying linear state-space models are powerful tools for obtaining mathematically interpretable representations of neural signals. For example, switching and decomposed models describe complex systems using latent variables that evolve according to simple locally linear dynamics. However, existing methods for latent variable estimation are not robust to dynamical noise and system nonlinearity due to noise-sensitive inference procedures and limited model formulations. This can lead to inconsistent results on signals with similar dynamics, limiting the model's ability to provide scientific insight. In this work, we address these limitations and propose a probabilistic approach to latent variable estimation in decomposed models that improves robustness against dynamical noise. Additionally, we introduce an extended latent dynamics model to improve robustness against system nonlinearities. We evaluate our approach on several synthetic dynamical systems, including an empirically-derived brain-computer interface experiment, and demonstrate more accurate latent variable inference in nonlinear systems with diverse noise conditions. Furthermore, we apply our method to a real-world clinical neurophysiology dataset, illustrating the ability to identify interpretable and coherent structure where previous models cannot.

Manifold Contrastive Learning with Variational Lie Group Operators

Self-supervised learning of deep neural networks has become a prevalent paradigm for learning representations that transfer to a variety of downstream tasks. Similar to proposed models of the ventral stream of biological vision, it is observed that these networks lead to a separation of category manifolds in the representations of the penultimate layer. Although this observation matches the manifold hypothesis of representation learning, current self-supervised approaches are limited in their ability to explicitly model this manifold. Indeed, current approaches often only apply augmentations from a pre-specified set of "positive pairs" during learning. In this work, we propose a contrastive learning approach that directly models the latent manifold using Lie group operators parameterized by coefficients with a sparsity-promoting prior. A variational distribution over these coefficients provides a generative model of the manifold, with samples which provide feature augmentations applicable both during contrastive training and downstream tasks. Additionally, learned coefficient distributions provide a quantification of which transformations are most likely at each point on the manifold while preserving identity. We demonstrate benefits in self-supervised benchmarks for image datasets, as well as a downstream semi-supervised task. In the former case, we demonstrate that the proposed methods can effectively apply manifold feature augmentations and improve learning both with and without a projection head. In the latter case, we demonstrate that feature augmentations sampled from learned Lie group operators can improve classification performance when using few labels.

PrefGen: Preference Guided Image Generation with Relative Attributes

Deep generative models have the capacity to render high fidelity images of content like human faces. Recently, there has been substantial progress in conditionally generating images with specific quantitative attributes, like the emotion conveyed by one's face. These methods typically require a user to explicitly quantify the desired intensity of a visual attribute. A limitation of this method is that many attributes, like how "angry" a human face looks, are difficult for a user to precisely quantify. However, a user would be able to reliably say which of two faces seems "angrier". Following this premise, we develop the $\textit{PrefGen}$ system, which allows users to control the relative attributes of generated images by presenting them with simple paired comparison queries of the form "do you prefer image $a$ or image $b$?" Using information from a sequence of query responses, we can estimate user preferences over a set of image attributes and perform preference-guided image editing and generation. Furthermore, to make preference localization feasible and efficient, we apply an active query selection strategy. We demonstrate the success of this approach using a StyleGAN2 generator on the task of human face editing. Additionally, we demonstrate how our approach can be combined with CLIP, allowing a user to edit the relative intensity of attributes specified by text prompts. Code at https://github.com/helblazer811/PrefGen.

Decomposed Linear Dynamical Systems (dLDS) for learning the latent components of neural dynamics

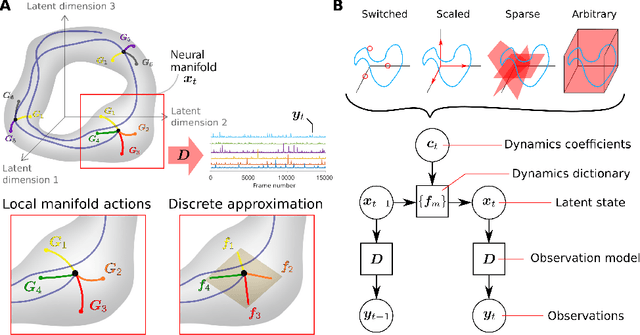
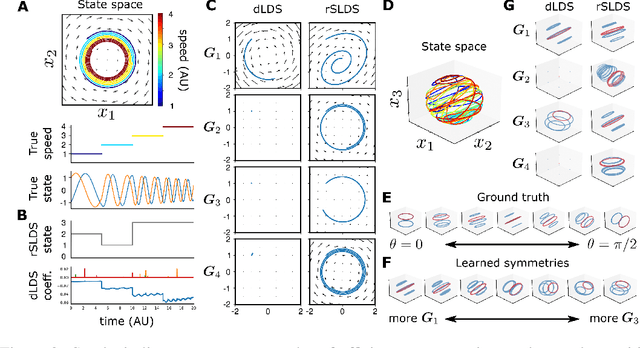
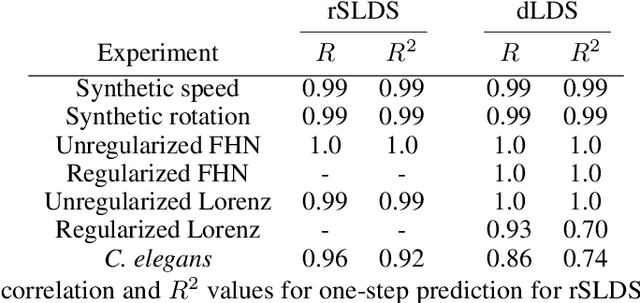
Learning interpretable representations of neural dynamics at a population level is a crucial first step to understanding how neural activity relates to perception and behavior. Models of neural dynamics often focus on either low-dimensional projections of neural activity, or on learning dynamical systems that explicitly relate to the neural state over time. We discuss how these two approaches are interrelated by considering dynamical systems as representative of flows on a low-dimensional manifold. Building on this concept, we propose a new decomposed dynamical system model that represents complex non-stationary and nonlinear dynamics of time-series data as a sparse combination of simpler, more interpretable components. The decomposed nature of the dynamics generalizes over previous switched approaches and enables modeling of overlapping and non-stationary drifts in the dynamics. We further present a dictionary learning-driven approach to model fitting, where we leverage recent results in tracking sparse vectors over time. We demonstrate that our model can learn efficient representations and smooth transitions between dynamical modes in both continuous-time and discrete-time examples. We show results on low-dimensional linear and nonlinear attractors to demonstrate that our decomposed dynamical systems model can well approximate nonlinear dynamics. Additionally, we apply our model to C. elegans data, illustrating a diversity of dynamics that is obscured when classified into discrete states.

Variational Sparse Coding with Learned Thresholding

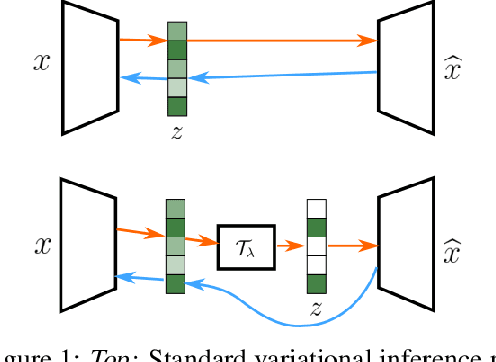
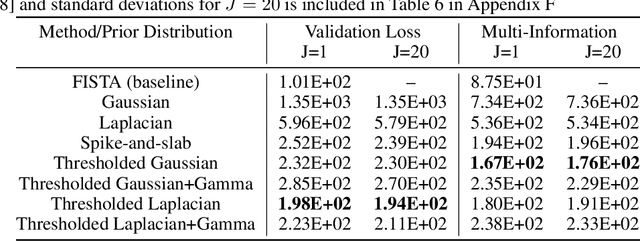
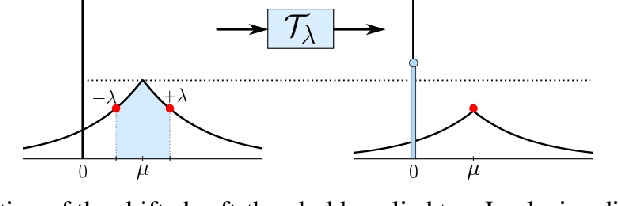
Sparse coding strategies have been lauded for their parsimonious representations of data that leverage low dimensional structure. However, inference of these codes typically relies on an optimization procedure with poor computational scaling in high-dimensional problems. For example, sparse inference in the representations learned in the high-dimensional intermediary layers of deep neural networks (DNNs) requires an iterative minimization to be performed at each training step. As such, recent, quick methods in variational inference have been proposed to infer sparse codes by learning a distribution over the codes with a DNN. In this work, we propose a new approach to variational sparse coding that allows us to learn sparse distributions by thresholding samples, avoiding the use of problematic relaxations. We first evaluate and analyze our method by training a linear generator, showing that it has superior performance, statistical efficiency, and gradient estimation compared to other sparse distributions. We then compare to a standard variational autoencoder using a DNN generator on the Fashion MNIST and CelebA datasets

Late fusion of machine learning models using passively captured interpersonal social interactions and motion from smartphones predicts decompensation in heart failure

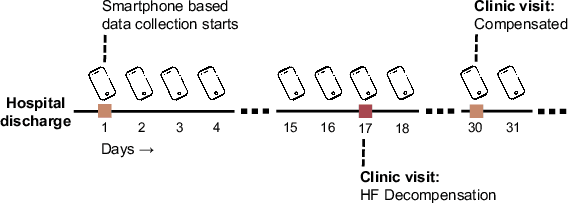
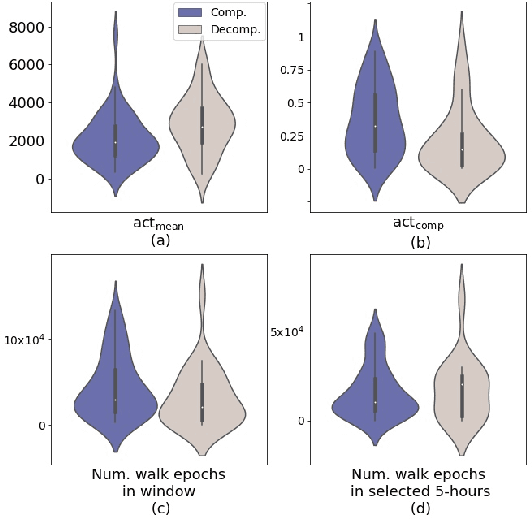
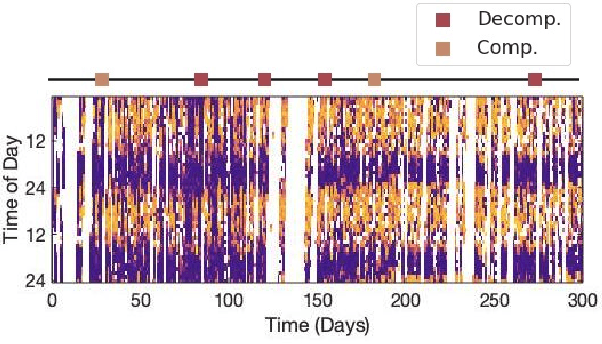
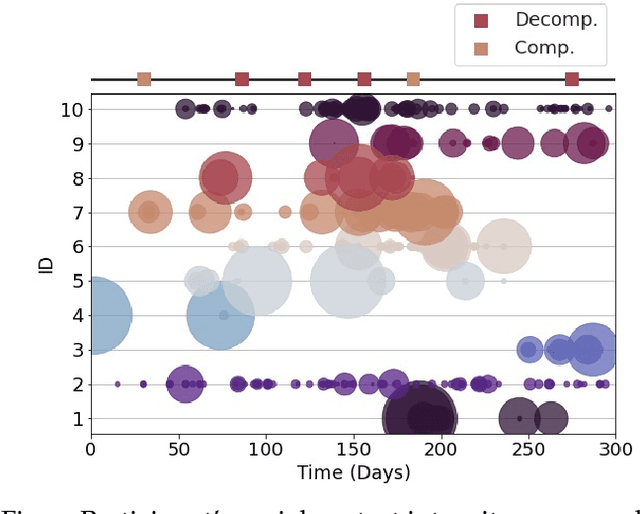
Objective: Worldwide, heart failure (HF) is a major cause of morbidity and mortality and one of the leading causes of hospitalization. Early detection of HF symptoms and pro-active management may reduce adverse events. Approach: Twenty-eight participants were monitored using a smartphone app after discharge from hospitals, and each clinical event during the enrollment (N=110 clinical events) was recorded. Motion, social, location, and clinical survey data collected via the smartphone-based monitoring system were used to develop and validate an algorithm for predicting or classifying HF decompensation events (hospitalizations or clinic visit) versus clinic monitoring visits in which they were determined to be compensated or stable. Models based on single modality as well as early and late fusion approaches combining patient-reported outcomes and passive smartphone data were evaluated. Results: The highest AUCPr for classifying decompensation with a late fusion approach was 0.80 using leave one subject out cross-validation. Significance: Passively collected data from smartphones, especially when combined with weekly patient-reported outcomes, may reflect behavioral and physiological changes due to HF and thus could enable prediction of HF decompensation.

Variational Autoencoder with Learned Latent Structure

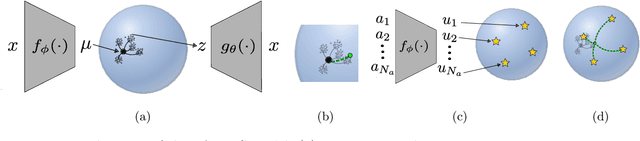
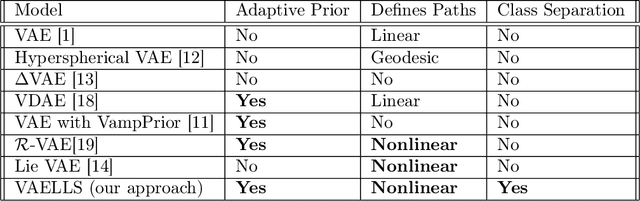
The manifold hypothesis states that high-dimensional data can be modeled as lying on or near a low-dimensional, nonlinear manifold. Variational Autoencoders (VAEs) approximate this manifold by learning mappings from low-dimensional latent vectors to high-dimensional data while encouraging a global structure in the latent space through the use of a specified prior distribution. When this prior does not match the structure of the true data manifold, it can lead to a less accurate model of the data. To resolve this mismatch, we introduce the Variational Autoencoder with Learned Latent Structure (VAELLS) which incorporates a learnable manifold model into the latent space of a VAE. This enables us to learn the nonlinear manifold structure from the data and use that structure to define a prior in the latent space. The integration of a latent manifold model not only ensures that our prior is well-matched to the data, but also allows us to define generative transformation paths in the latent space and describe class manifolds by transformations stemming from examples of each class. We validate our model on examples with known latent structure and also demonstrate its capabilities on a real-world dataset.

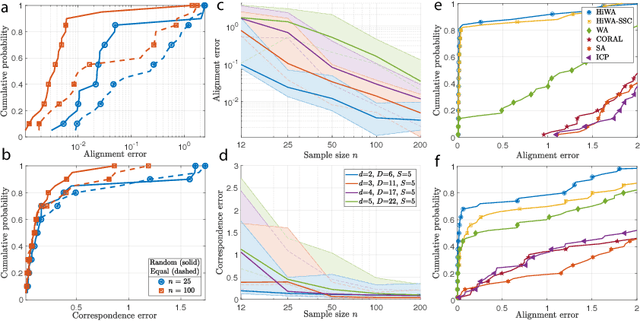
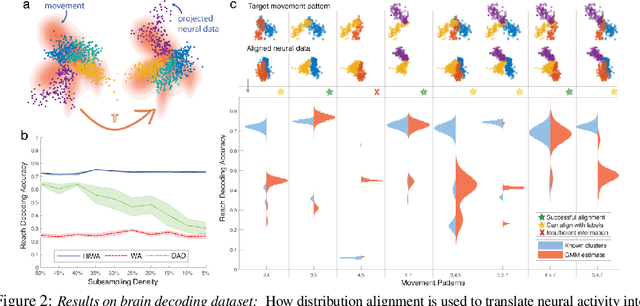
Hierarchical Optimal Transport for Multimodal Distribution Alignment

In many machine learning applications, it is necessary to meaningfully aggregate, through alignment, different but related datasets. Optimal transport (OT)-based approaches pose alignment as a divergence minimization problem: the aim is to transform a source dataset to match a target dataset using the Wasserstein distance as a divergence measure. We introduce a hierarchical formulation of OT which leverages clustered structure in data to improve alignment in noisy, ambiguous, or multimodal settings. To solve this numerically, we propose a distributed ADMM algorithm that also exploits the Sinkhorn distance, thus it has an efficient computational complexity that scales quadratically with the size of the largest cluster. When the transformation between two datasets is unitary, we provide performance guarantees that describe when and how well aligned cluster correspondences can be recovered with our formulation, as well as provide worst-case dataset geometry for such a strategy. We apply this method to synthetic datasets that model data as mixtures of low-rank Gaussians and study the impact that different geometric properties of the data have on alignment. Next, we applied our approach to a neural decoding application where the goal is to predict movement directions and instantaneous velocities from populations of neurons in the macaque primary motor cortex. Our results demonstrate that when clustered structure exists in datasets, and is consistent across trials or time points, a hierarchical alignment strategy that leverages such structure can provide significant improvements in cross-domain alignment.

Active embedding search via noisy paired comparisons

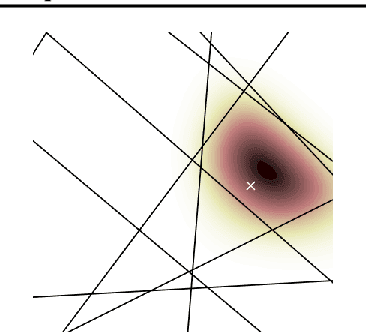
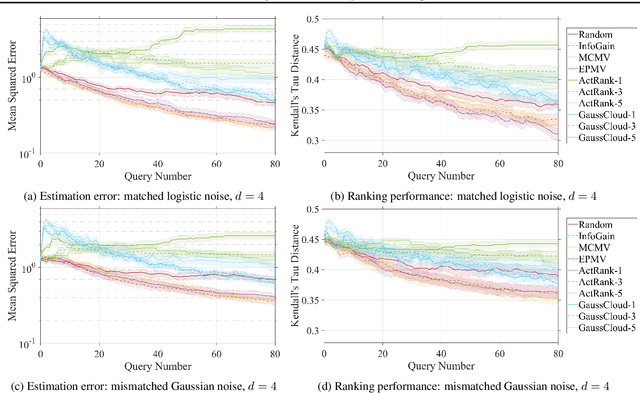
Suppose that we wish to estimate a user's preference vector $w$ from paired comparisons of the form "does user $w$ prefer item $p$ or item $q$?," where both the user and items are embedded in a low-dimensional Euclidean space with distances that reflect user and item similarities. Such observations arise in numerous settings, including psychometrics and psychology experiments, search tasks, advertising, and recommender systems. In such tasks, queries can be extremely costly and subject to varying levels of response noise; thus, we aim to actively choose pairs that are most informative given the results of previous comparisons. We provide new theoretical insights into the benefits and challenges of greedy information maximization in this setting, and develop two novel strategies that maximize lower bounds on information gain and are simpler to analyze and compute respectively. We use simulated responses from a real-world dataset to validate our strategies through their similar performance to greedy information maximization, and their superior preference estimation over state-of-the-art selection methods as well as random queries.

Short Term Memory Capacity in Networks via the Restricted Isometry Property

Cortical networks are hypothesized to rely on transient network activity to support short term memory (STM). In this paper we study the capacity of randomly connected recurrent linear networks for performing STM when the input signals are approximately sparse in some basis. We leverage results from compressed sensing to provide rigorous non asymptotic recovery guarantees, quantifying the impact of the input sparsity level, the input sparsity basis, and the network characteristics on the system capacity. Our analysis demonstrates that network memory capacities can scale superlinearly with the number of nodes, and in some situations can achieve STM capacities that are much larger than the network size. We provide perfect recovery guarantees for finite sequences and recovery bounds for infinite sequences. The latter analysis predicts that network STM systems may have an optimal recovery length that balances errors due to omission and recall mistakes. Furthermore, we show that the conditions yielding optimal STM capacity can be embodied in several network topologies, including networks with sparse or dense connectivities.