Andrew K. Massimino
Active embedding search via noisy paired comparisons
May 24, 2019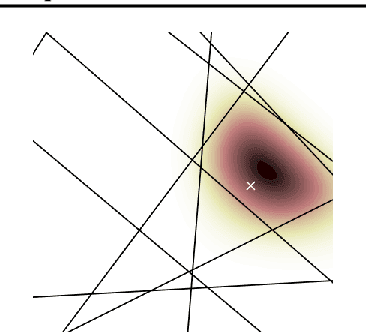
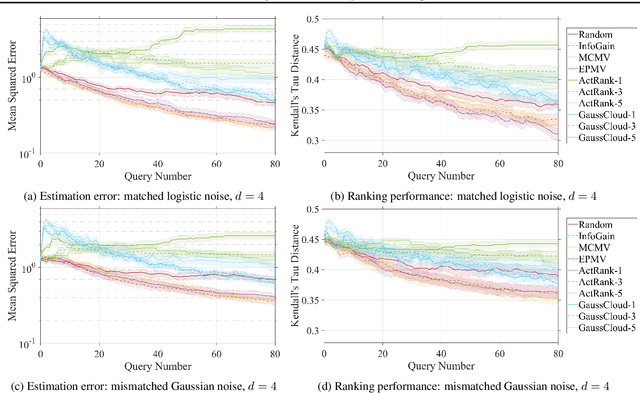
Abstract:Suppose that we wish to estimate a user's preference vector $w$ from paired comparisons of the form "does user $w$ prefer item $p$ or item $q$?," where both the user and items are embedded in a low-dimensional Euclidean space with distances that reflect user and item similarities. Such observations arise in numerous settings, including psychometrics and psychology experiments, search tasks, advertising, and recommender systems. In such tasks, queries can be extremely costly and subject to varying levels of response noise; thus, we aim to actively choose pairs that are most informative given the results of previous comparisons. We provide new theoretical insights into the benefits and challenges of greedy information maximization in this setting, and develop two novel strategies that maximize lower bounds on information gain and are simpler to analyze and compute respectively. We use simulated responses from a real-world dataset to validate our strategies through their similar performance to greedy information maximization, and their superior preference estimation over state-of-the-art selection methods as well as random queries.
As you like it: Localization via paired comparisons
Feb 19, 2018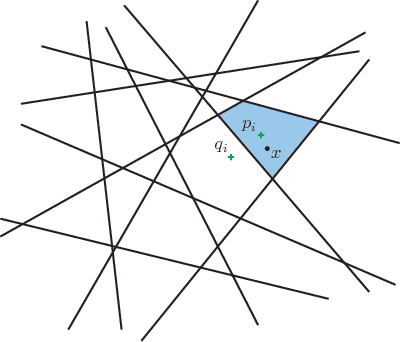
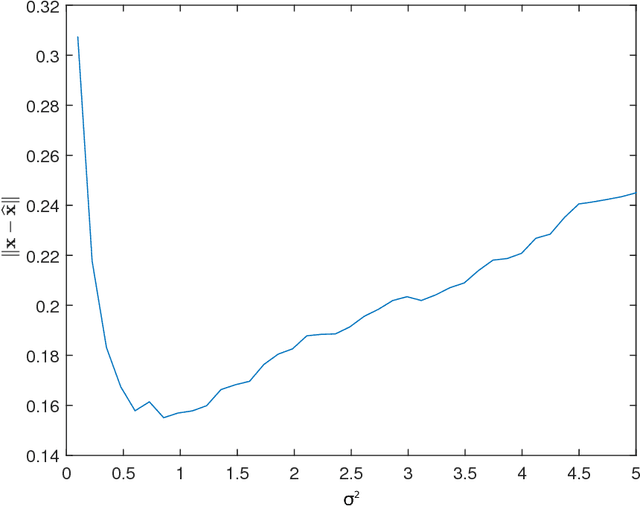
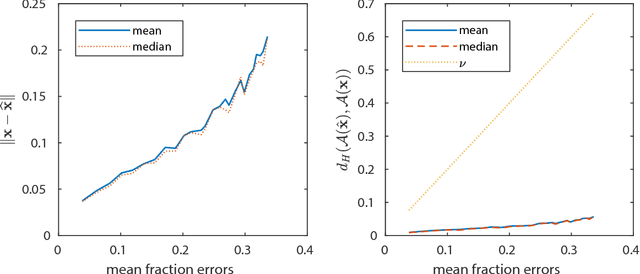
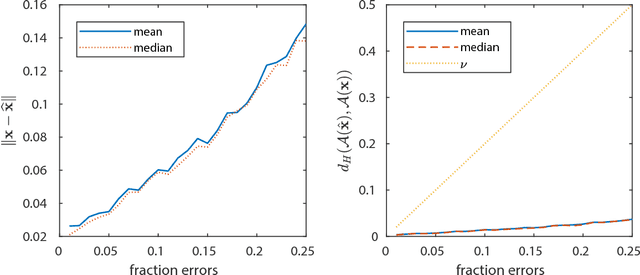
Abstract:Suppose that we wish to estimate a vector $\mathbf{x}$ from a set of binary paired comparisons of the form "$\mathbf{x}$ is closer to $\mathbf{p}$ than to $\mathbf{q}$" for various choices of vectors $\mathbf{p}$ and $\mathbf{q}$. The problem of estimating $\mathbf{x}$ from this type of observation arises in a variety of contexts, including nonmetric multidimensional scaling, "unfolding," and ranking problems, often because it provides a powerful and flexible model of preference. We describe theoretical bounds for how well we can expect to estimate $\mathbf{x}$ under a randomized model for $\mathbf{p}$ and $\mathbf{q}$. We also present results for the case where the comparisons are noisy and subject to some degree of error. Additionally, we show that under a randomized model for $\mathbf{p}$ and $\mathbf{q}$, a suitable number of binary paired comparisons yield a stable embedding of the space of target vectors. Finally, we also that we can achieve significant gains by adaptively changing the distribution for choosing $\mathbf{p}$ and $\mathbf{q}$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge