Variational Autoencoder with Learned Latent Structure
Paper and Code
Jun 18, 2020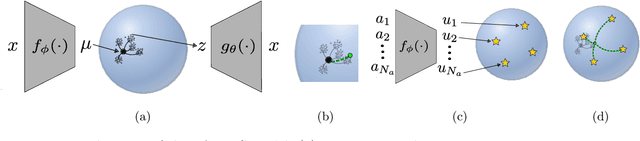
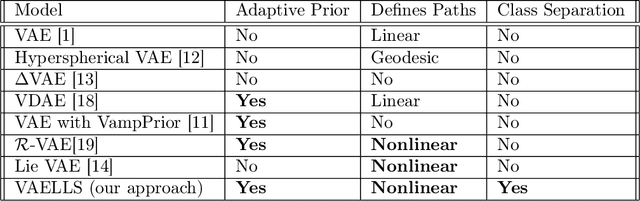


The manifold hypothesis states that high-dimensional data can be modeled as lying on or near a low-dimensional, nonlinear manifold. Variational Autoencoders (VAEs) approximate this manifold by learning mappings from low-dimensional latent vectors to high-dimensional data while encouraging a global structure in the latent space through the use of a specified prior distribution. When this prior does not match the structure of the true data manifold, it can lead to a less accurate model of the data. To resolve this mismatch, we introduce the Variational Autoencoder with Learned Latent Structure (VAELLS) which incorporates a learnable manifold model into the latent space of a VAE. This enables us to learn the nonlinear manifold structure from the data and use that structure to define a prior in the latent space. The integration of a latent manifold model not only ensures that our prior is well-matched to the data, but also allows us to define generative transformation paths in the latent space and describe class manifolds by transformations stemming from examples of each class. We validate our model on examples with known latent structure and also demonstrate its capabilities on a real-world dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge