Decomposed Linear Dynamical Systems (dLDS) for learning the latent components of neural dynamics
Paper and Code
Jun 07, 2022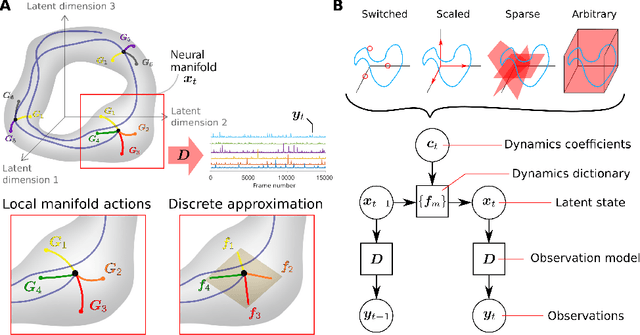

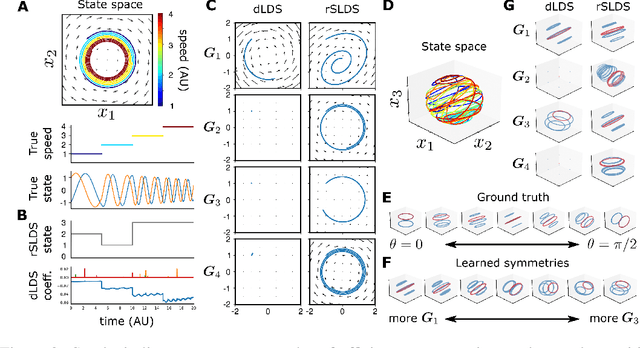
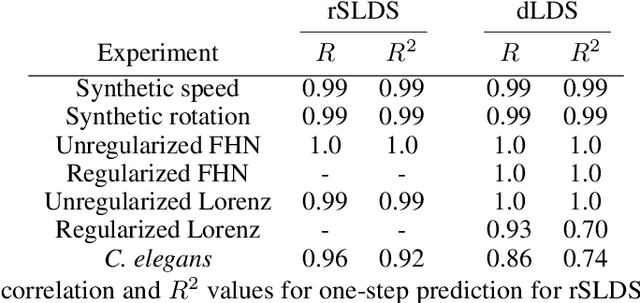
Learning interpretable representations of neural dynamics at a population level is a crucial first step to understanding how neural activity relates to perception and behavior. Models of neural dynamics often focus on either low-dimensional projections of neural activity, or on learning dynamical systems that explicitly relate to the neural state over time. We discuss how these two approaches are interrelated by considering dynamical systems as representative of flows on a low-dimensional manifold. Building on this concept, we propose a new decomposed dynamical system model that represents complex non-stationary and nonlinear dynamics of time-series data as a sparse combination of simpler, more interpretable components. The decomposed nature of the dynamics generalizes over previous switched approaches and enables modeling of overlapping and non-stationary drifts in the dynamics. We further present a dictionary learning-driven approach to model fitting, where we leverage recent results in tracking sparse vectors over time. We demonstrate that our model can learn efficient representations and smooth transitions between dynamical modes in both continuous-time and discrete-time examples. We show results on low-dimensional linear and nonlinear attractors to demonstrate that our decomposed dynamical systems model can well approximate nonlinear dynamics. Additionally, we apply our model to C. elegans data, illustrating a diversity of dynamics that is obscured when classified into discrete states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge