LINOCS: Lookahead Inference of Networked Operators for Continuous Stability

Identifying latent interactions within complex systems is key to unlocking deeper insights into their operational dynamics, including how their elements affect each other and contribute to the overall system behavior. For instance, in neuroscience, discovering neuron-to-neuron interactions is essential for understanding brain function; in ecology, recognizing the interactions among populations is key for understanding complex ecosystems. Such systems, often modeled as dynamical systems, typically exhibit noisy high-dimensional and non-stationary temporal behavior that renders their identification challenging. Existing dynamical system identification methods often yield operators that accurately capture short-term behavior but fail to predict long-term trends, suggesting an incomplete capture of the underlying process. Methods that consider extended forecasts (e.g., recurrent neural networks) lack explicit representations of element-wise interactions and require substantial training data, thereby failing to capture interpretable network operators. Here we introduce Lookahead-driven Inference of Networked Operators for Continuous Stability (LINOCS), a robust learning procedure for identifying hidden dynamical interactions in noisy time-series data. LINOCS integrates several multi-step predictions with adaptive weights during training to recover dynamical operators that can yield accurate long-term predictions. We demonstrate LINOCS' ability to recover the ground truth dynamical operators underlying synthetic time-series data for multiple dynamical systems models (including linear, piece-wise linear, time-changing linear systems' decomposition, and regularized linear time-varying systems) as well as its capability to produce meaningful operators with robust reconstructions through various real-world examples.

Decomposed Linear Dynamical Systems (dLDS) for learning the latent components of neural dynamics

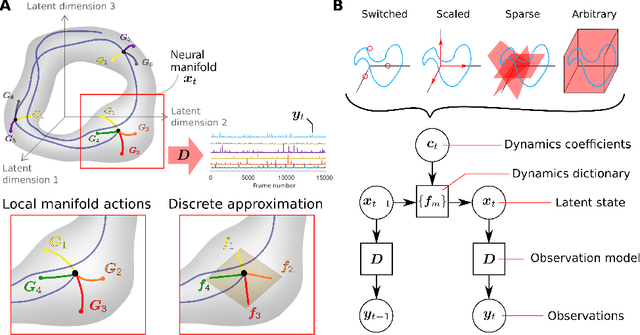
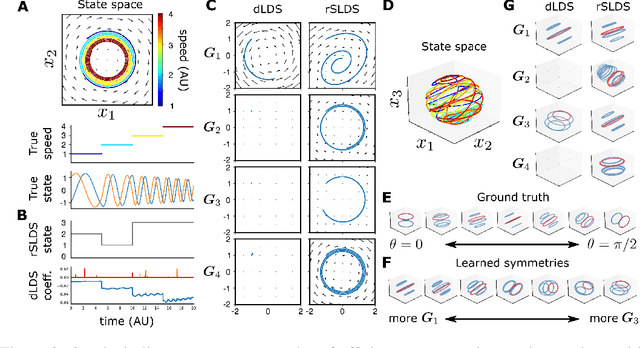
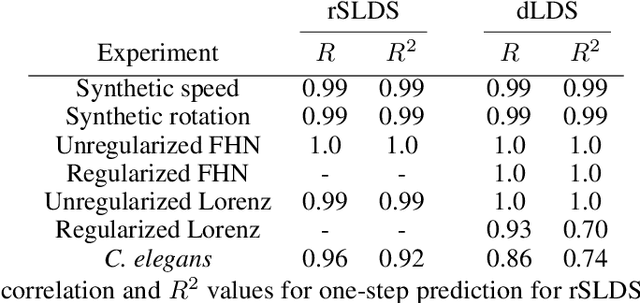
Learning interpretable representations of neural dynamics at a population level is a crucial first step to understanding how neural activity relates to perception and behavior. Models of neural dynamics often focus on either low-dimensional projections of neural activity, or on learning dynamical systems that explicitly relate to the neural state over time. We discuss how these two approaches are interrelated by considering dynamical systems as representative of flows on a low-dimensional manifold. Building on this concept, we propose a new decomposed dynamical system model that represents complex non-stationary and nonlinear dynamics of time-series data as a sparse combination of simpler, more interpretable components. The decomposed nature of the dynamics generalizes over previous switched approaches and enables modeling of overlapping and non-stationary drifts in the dynamics. We further present a dictionary learning-driven approach to model fitting, where we leverage recent results in tracking sparse vectors over time. We demonstrate that our model can learn efficient representations and smooth transitions between dynamical modes in both continuous-time and discrete-time examples. We show results on low-dimensional linear and nonlinear attractors to demonstrate that our decomposed dynamical systems model can well approximate nonlinear dynamics. Additionally, we apply our model to C. elegans data, illustrating a diversity of dynamics that is obscured when classified into discrete states.

Prospective Learning: Back to the Future

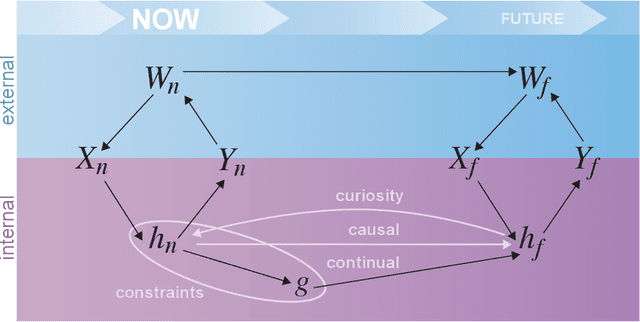
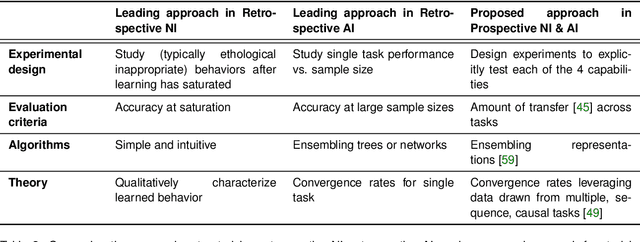
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.