LINOCS: Lookahead Inference of Networked Operators for Continuous Stability

Identifying latent interactions within complex systems is key to unlocking deeper insights into their operational dynamics, including how their elements affect each other and contribute to the overall system behavior. For instance, in neuroscience, discovering neuron-to-neuron interactions is essential for understanding brain function; in ecology, recognizing the interactions among populations is key for understanding complex ecosystems. Such systems, often modeled as dynamical systems, typically exhibit noisy high-dimensional and non-stationary temporal behavior that renders their identification challenging. Existing dynamical system identification methods often yield operators that accurately capture short-term behavior but fail to predict long-term trends, suggesting an incomplete capture of the underlying process. Methods that consider extended forecasts (e.g., recurrent neural networks) lack explicit representations of element-wise interactions and require substantial training data, thereby failing to capture interpretable network operators. Here we introduce Lookahead-driven Inference of Networked Operators for Continuous Stability (LINOCS), a robust learning procedure for identifying hidden dynamical interactions in noisy time-series data. LINOCS integrates several multi-step predictions with adaptive weights during training to recover dynamical operators that can yield accurate long-term predictions. We demonstrate LINOCS' ability to recover the ground truth dynamical operators underlying synthetic time-series data for multiple dynamical systems models (including linear, piece-wise linear, time-changing linear systems' decomposition, and regularized linear time-varying systems) as well as its capability to produce meaningful operators with robust reconstructions through various real-world examples.

Distance preservation in state-space methods for detecting causal interactions in dynamical systems

We analyze the popular ``state-space'' class of algorithms for detecting casual interaction in coupled dynamical systems. These algorithms are often justified by Takens' embedding theorem, which provides conditions under which relationships involving attractors and their delay embeddings are continuous. In practice, however, state-space methods often do not directly test continuity, but rather the stronger property of how these relationships preserve inter-point distances. This paper theoretically and empirically explores state-space algorithms explicitly from the perspective of distance preservation. We first derive basic theoretical guarantees applicable to simple coupled systems, providing conditions under which the distance preservation of a certain map reveals underlying causal structure. Second, we demonstrate empirically that typical coupled systems do not satisfy distance preservation assumptions. Taken together, our results underline the dependence of state-space algorithms on intrinsic system properties and the relationship between the system and the function used to measure it -- properties that are not directly associated with causal interaction.

Learning Internal Representations of 3D Transformations from 2D Projected Inputs

When interacting in a three dimensional world, humans must estimate 3D structure from visual inputs projected down to two dimensional retinal images. It has been shown that humans use the persistence of object shape over motion-induced transformations as a cue to resolve depth ambiguity when solving this underconstrained problem. With the aim of understanding how biological vision systems may internally represent 3D transformations, we propose a computational model, based on a generative manifold model, which can be used to infer 3D structure from the motion of 2D points. Our model can also learn representations of the transformations with minimal supervision, providing a proof of concept for how humans may develop internal representations on a developmental or evolutionary time scale. Focused on rotational motion, we show how our model infers depth from moving 2D projected points, learns 3D rotational transformations from 2D training stimuli, and compares to human performance on psychophysical structure-from-motion experiments.

A Low-complexity Brain-computer Interface for High-complexity Robot Swarm Control

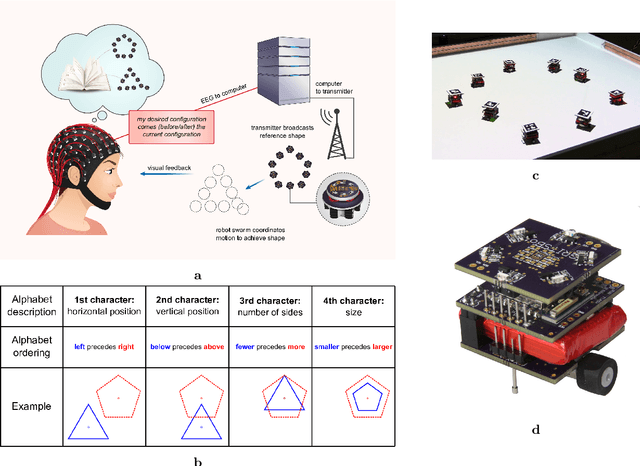
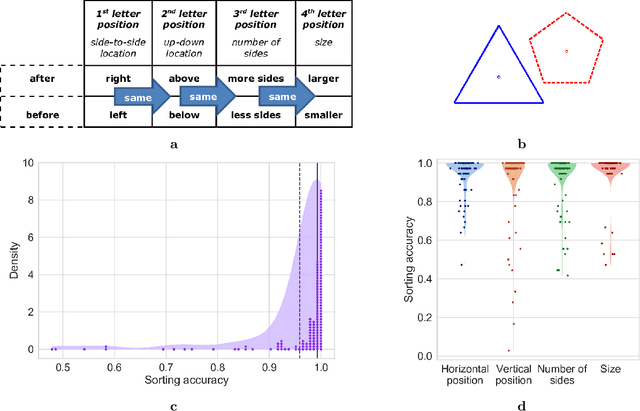
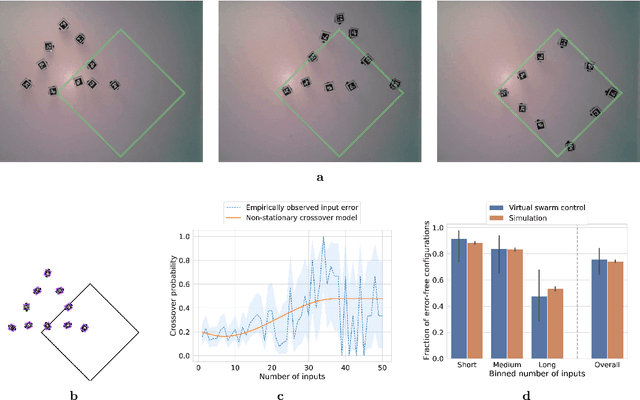
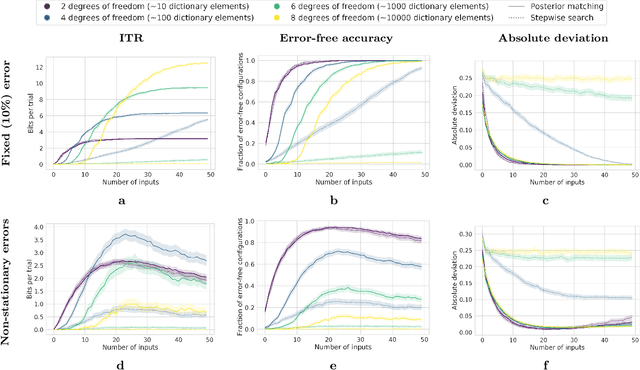
A brain-computer interface (BCI) is a system that allows a human operator to use only mental commands in controlling end effectors that interact with the world around them. Such a system consists of a measurement device to record the human user's brain activity, which is then processed into commands that drive a system end effector. BCIs involve either invasive measurements which allow for high-complexity control but are generally infeasible, or noninvasive measurements which offer lower quality signals but are more practical to use. In general, BCI systems have not been developed that efficiently, robustly, and scalably perform high-complexity control while retaining the practicality of noninvasive measurements. Here we leverage recent results from feedback information theory to fill this gap by modeling BCIs as a communications system and deploying a human-implementable interaction algorithm for noninvasive control of a high-complexity robot swarm. We construct a scalable dictionary of robotic behaviors that can be searched simply and efficiently by a BCI user, as we demonstrate through a large-scale user study testing the feasibility of our interaction algorithm, a user test of the full BCI system on (virtual and real) robot swarms, and simulations that verify our results against theoretical models. Our results provide a proof of concept for how a large class of high-complexity effectors (even beyond robotics) can be effectively controlled by a BCI system with low-complexity and noisy inputs.

Learning Identity-Preserving Transformations on Data Manifolds

Many machine learning techniques incorporate identity-preserving transformations into their models to generalize their performance to previously unseen data. These transformations are typically selected from a set of functions that are known to maintain the identity of an input when applied (e.g., rotation, translation, flipping, and scaling). However, there are many natural variations that cannot be labeled for supervision or defined through examination of the data. As suggested by the manifold hypothesis, many of these natural variations live on or near a low-dimensional, nonlinear manifold. Several techniques represent manifold variations through a set of learned Lie group operators that define directions of motion on the manifold. However theses approaches are limited because they require transformation labels when training their models and they lack a method for determining which regions of the manifold are appropriate for applying each specific operator. We address these limitations by introducing a learning strategy that does not require transformation labels and developing a method that learns the local regions where each operator is likely to be used while preserving the identity of inputs. Experiments on MNIST and Fashion MNIST highlight our model's ability to learn identity-preserving transformations on multi-class datasets. Additionally, we train on CelebA to showcase our model's ability to learn semantically meaningful transformations on complex datasets in an unsupervised manner.

Feedback Coding for Active Learning

The iterative selection of examples for labeling in active machine learning is conceptually similar to feedback channel coding in information theory: in both tasks, the objective is to seek a minimal sequence of actions to encode information in the presence of noise. While this high-level overlap has been previously noted, there remain open questions on how to best formulate active learning as a communications system to leverage existing analysis and algorithms in feedback coding. In this work, we formally identify and leverage the structural commonalities between the two problems, including the characterization of encoder and noisy channel components, to design a new algorithm. Specifically, we develop an optimal transport-based feedback coding scheme called Approximate Posterior Matching (APM) for the task of active example selection and explore its application to Bayesian logistic regression, a popular model in active learning. We evaluate APM on a variety of datasets and demonstrate learning performance comparable to existing active learning methods, at a reduced computational cost. These results demonstrate the potential of directly deploying concepts from feedback channel coding to design efficient active learning strategies.

Generative causal explanations of black-box classifiers

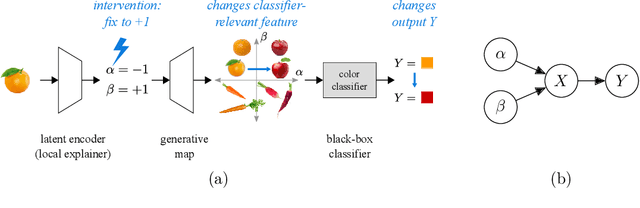
We develop a method for generating causal post-hoc explanations of black-box classifiers based on a learned low-dimensional representation of the data. The explanation is causal in the sense that changing learned latent factors produces a change in the classifier output statistics. To construct these explanations, we design a learning framework that leverages a generative model and information-theoretic measures of causal influence. Our objective function encourages both the generative model to faithfully represent the data distribution and the latent factors to have a large causal influence on the classifier output. Our method learns both global and local explanations, is compatible with any classifier that admits class probabilities and a gradient, and does not require labeled attributes or knowledge of causal structure. Using carefully controlled test cases, we provide intuition that illuminates the function of our causal objective. We then demonstrate the practical utility of our method on image recognition tasks.

Representing Closed Transformation Paths in Encoded Network Latent Space

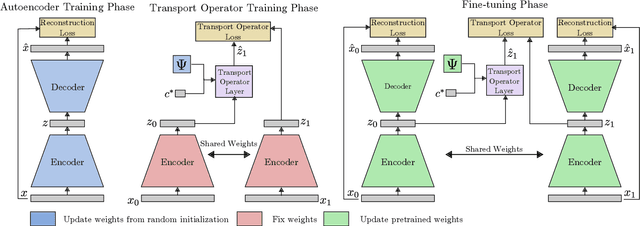
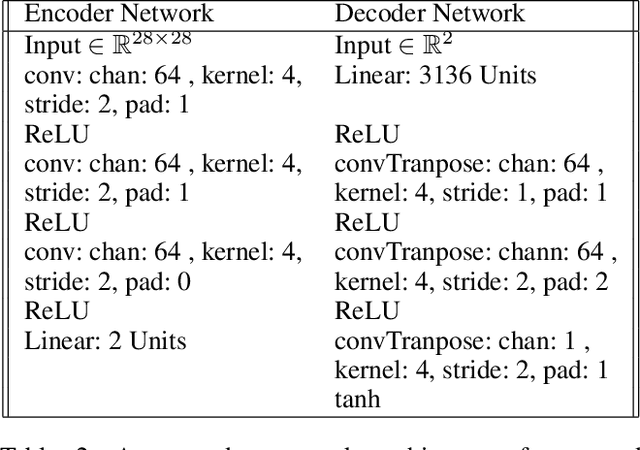
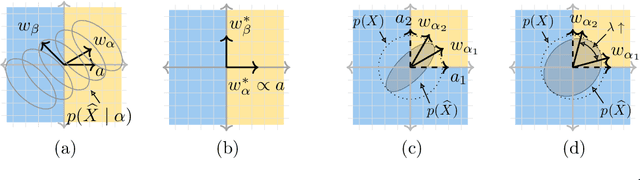
Deep generative networks have been widely used for learning mappings from a low-dimensional latent space to a high-dimensional data space. In many cases, data transformations are defined by linear paths in this latent space. However, the Euclidean structure of the latent space may be a poor match for the underlying latent structure in the data. In this work, we incorporate a generative manifold model into the latent space of an autoencoder in order to learn the low-dimensional manifold structure from the data and adapt the latent space to accommodate this structure. In particular, we focus on applications in which the data has closed transformation paths which extend from a starting point and return to nearly the same point. Through experiments on data with natural closed transformation paths, we show that this model introduces the ability to learn the latent dynamics of complex systems, generate transformation paths, and classify samples that belong on the same transformation path.

Active Ordinal Querying for Tuplewise Similarity Learning

Many machine learning tasks such as clustering, classification, and dataset search benefit from embedding data points in a space where distances reflect notions of relative similarity as perceived by humans. A common way to construct such an embedding is to request triplet similarity queries to an oracle, comparing two objects with respect to a reference. This work generalizes triplet queries to tuple queries of arbitrary size that ask an oracle to rank multiple objects against a reference, and introduces an efficient and robust adaptive selection method called InfoTuple that uses a novel approach to mutual information maximization. We show that the performance of InfoTuple at various tuple sizes exceeds that of the state-of-the-art adaptive triplet selection method on synthetic tests and new human response datasets, and empirically demonstrate the significant gains in efficiency and query consistency achieved by querying larger tuples instead of triplets.

Distributed Sequence Memory of Multidimensional Inputs in Recurrent Networks

Recurrent neural networks (RNNs) have drawn interest from machine learning researchers because of their effectiveness at preserving past inputs for time-varying data processing tasks. To understand the success and limitations of RNNs, it is critical that we advance our analysis of their fundamental memory properties. We focus on echo state networks (ESNs), which are RNNs with simple memoryless nodes and random connectivity. In most existing analyses, the short-term memory (STM) capacity results conclude that the ESN network size must scale linearly with the input size for unstructured inputs. The main contribution of this paper is to provide general results characterizing the STM capacity for linear ESNs with multidimensional input streams when the inputs have common low-dimensional structure: sparsity in a basis or significant statistical dependence between inputs. In both cases, we show that the number of nodes in the network must scale linearly with the information rate and poly-logarithmically with the ambient input dimension. The analysis relies on advanced applications of random matrix theory and results in explicit non-asymptotic bounds on the recovery error. Taken together, this analysis provides a significant step forward in our understanding of the STM properties in RNNs.