Manifold Alignment with Feature Correspondence

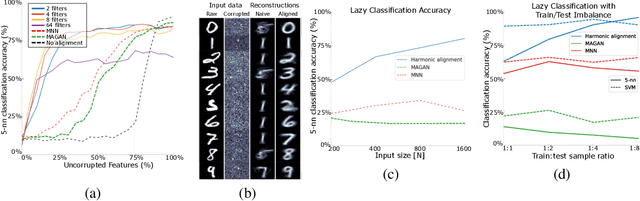
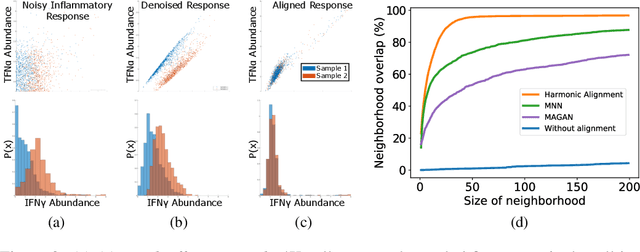
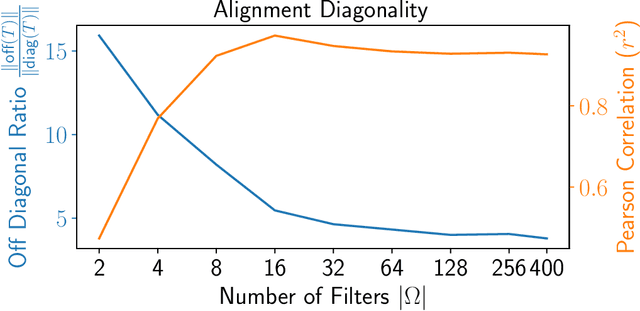
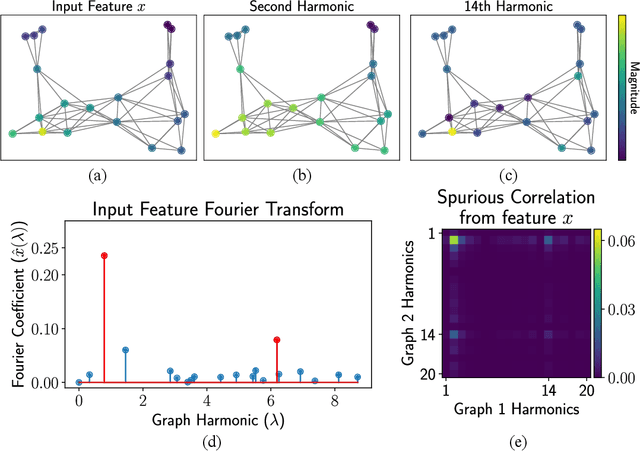
We propose a novel framework for combining datasets via alignment of their associated intrinsic dimensions. Our approach assumes that two datasets are sampled from a common latent space, i.e., they measure equivalent systems. Thus, we expect there to exist a natural (albeit unknown) alignment of the data manifolds associated with the intrinsic geometry of these datasets, which are perturbed by measurement artifacts in the sampling process. Importantly, we do not assume any individual correspondence (partial or complete) between data points. Instead, we rely on our assumption that a subset of data features have correspondence across datasets. We leverage this assumption to estimate relations between intrinsic manifold dimensions, which are given by diffusion map coordinates over each of the datasets. We compute a correlation matrix between diffusion coordinates of the datasets by considering graph (or manifold) Fourier coefficients of corresponding data features. We then orthogonalize this correlation matrix to form an isometric transformation between the diffusion maps of the datasets. Finally, we apply this transformation to the diffusion coordinates and construct a unified diffusion geometry of the datasets together. We show that this approach successfully corrects misalignment artifacts and enables data integration.