Xinshi Chen
Protenix-Mini: Efficient Structure Predictor via Compact Architecture, Few-Step Diffusion and Switchable pLM
Jul 16, 2025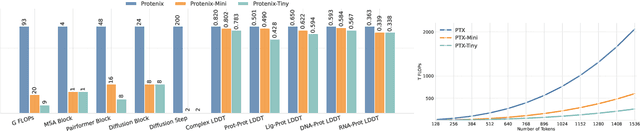



Abstract:Lightweight inference is critical for biomolecular structure prediction and other downstream tasks, enabling efficient real-world deployment and inference-time scaling for large-scale applications. In this work, we address the challenge of balancing model efficiency and prediction accuracy by making several key modifications, 1) Multi-step AF3 sampler is replaced by a few-step ODE sampler, significantly reducing computational overhead for the diffusion module part during inference; 2) In the open-source Protenix framework, a subset of pairformer or diffusion transformer blocks doesn't make contributions to the final structure prediction, presenting opportunities for architectural pruning and lightweight redesign; 3) A model incorporating an ESM module is trained to substitute the conventional MSA module, reducing MSA preprocessing time. Building on these key insights, we present Protenix-Mini, a compact and optimized model designed for efficient protein structure prediction. This streamlined version incorporates a more efficient architectural design with a two-step Ordinary Differential Equation (ODE) sampling strategy. By eliminating redundant Transformer components and refining the sampling process, Protenix-Mini significantly reduces model complexity with slight accuracy drop. Evaluations on benchmark datasets demonstrate that it achieves high-fidelity predictions, with only a negligible 1 to 5 percent decrease in performance on benchmark datasets compared to its full-scale counterpart. This makes Protenix-Mini an ideal choice for applications where computational resources are limited but accurate structure prediction remains crucial.
Graph Condensation via Receptive Field Distribution Matching
Jun 28, 2022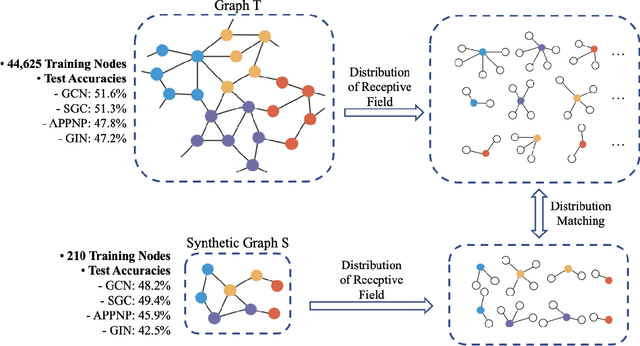

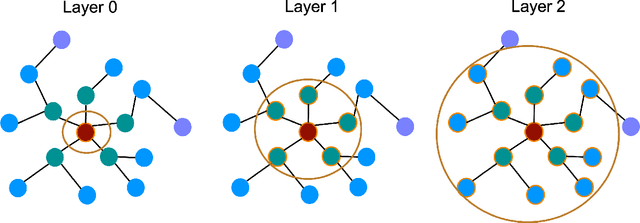
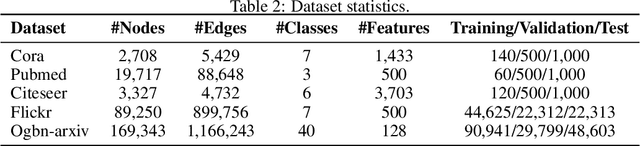
Abstract:Graph neural networks (GNNs) enable the analysis of graphs using deep learning, with promising results in capturing structured information in graphs. This paper focuses on creating a small graph to represent the original graph, so that GNNs trained on the size-reduced graph can make accurate predictions. We view the original graph as a distribution of receptive fields and aim to synthesize a small graph whose receptive fields share a similar distribution. Thus, we propose Graph Condesation via Receptive Field Distribution Matching (GCDM), which is accomplished by optimizing the synthetic graph through the use of a distribution matching loss quantified by maximum mean discrepancy (MMD). Additionally, we demonstrate that the synthetic graph generated by GCDM is highly generalizable to a variety of models in evaluation phase and that the condensing speed is significantly improved using this framework.
uGLAD: Sparse graph recovery by optimizing deep unrolled networks
May 23, 2022
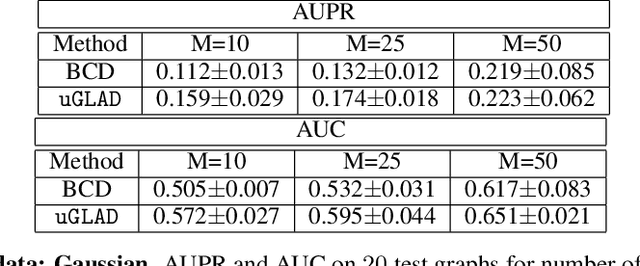
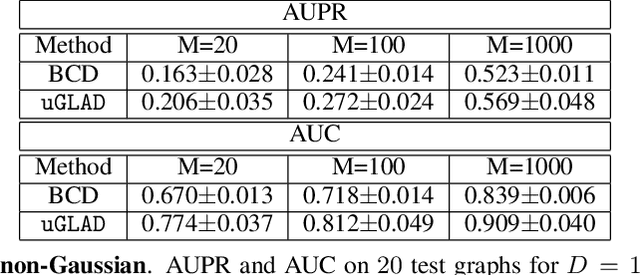

Abstract:Probabilistic Graphical Models (PGMs) are generative models of complex systems. They rely on conditional independence assumptions between variables to learn sparse representations which can be visualized in a form of a graph. Such models are used for domain exploration and structure discovery in poorly understood domains. This work introduces a novel technique to perform sparse graph recovery by optimizing deep unrolled networks. Assuming that the input data $X\in\mathbb{R}^{M\times D}$ comes from an underlying multivariate Gaussian distribution, we apply a deep model on $X$ that outputs the precision matrix $\Theta$, which can also be interpreted as the adjacency matrix. Our model, uGLAD, builds upon and extends the state-of-the-art model GLAD to the unsupervised setting. The key benefits of our model are (1) uGLAD automatically optimizes sparsity-related regularization parameters leading to better performance than existing algorithms. (2) We introduce multi-task learning based `consensus' strategy for robust handling of missing data in an unsupervised setting. We evaluate model results on synthetic Gaussian data, non-Gaussian data generated from Gene Regulatory Networks, and present a case study in anaerobic digestion.
Efficient Dynamic Graph Representation Learning at Scale
Dec 14, 2021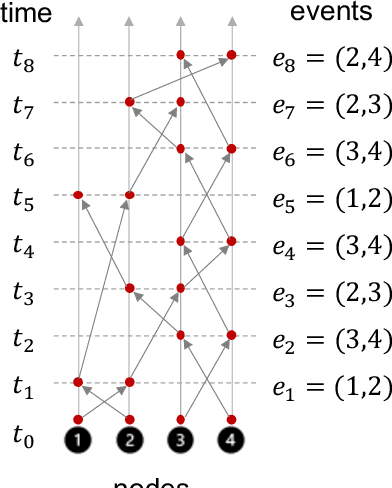
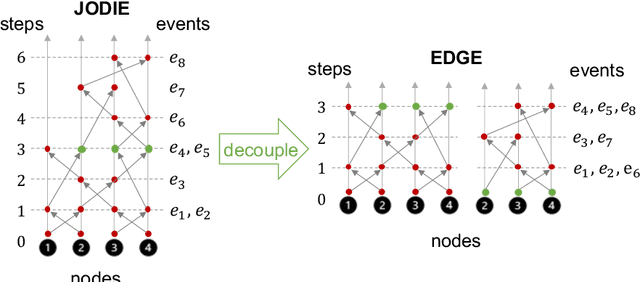
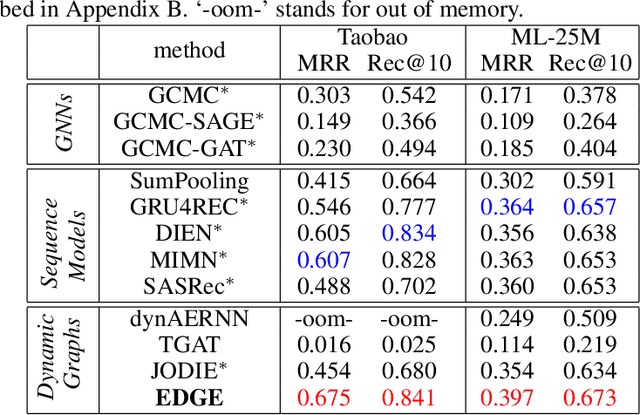
Abstract:Dynamic graphs with ordered sequences of events between nodes are prevalent in real-world industrial applications such as e-commerce and social platforms. However, representation learning for dynamic graphs has posed great computational challenges due to the time and structure dependency and irregular nature of the data, preventing such models from being deployed to real-world applications. To tackle this challenge, we propose an efficient algorithm, Efficient Dynamic Graph lEarning (EDGE), which selectively expresses certain temporal dependency via training loss to improve the parallelism in computations. We show that EDGE can scale to dynamic graphs with millions of nodes and hundreds of millions of temporal events and achieve new state-of-the-art (SOTA) performance.
Multi-task Learning of Order-Consistent Causal Graphs
Nov 03, 2021


Abstract:We consider the problem of discovering $K$ related Gaussian directed acyclic graphs (DAGs), where the involved graph structures share a consistent causal order and sparse unions of supports. Under the multi-task learning setting, we propose a $l_1/l_2$-regularized maximum likelihood estimator (MLE) for learning $K$ linear structural equation models. We theoretically show that the joint estimator, by leveraging data across related tasks, can achieve a better sample complexity for recovering the causal order (or topological order) than separate estimations. Moreover, the joint estimator is able to recover non-identifiable DAGs, by estimating them together with some identifiable DAGs. Lastly, our analysis also shows the consistency of union support recovery of the structures. To allow practical implementation, we design a continuous optimization problem whose optimizer is the same as the joint estimator and can be approximated efficiently by an iterative algorithm. We validate the theoretical analysis and the effectiveness of the joint estimator in experiments.
Understanding Deep Architectures with Reasoning Layer
Jun 24, 2020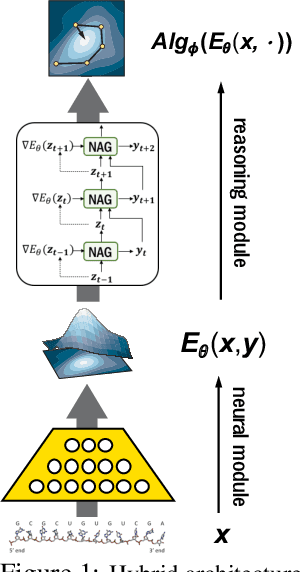

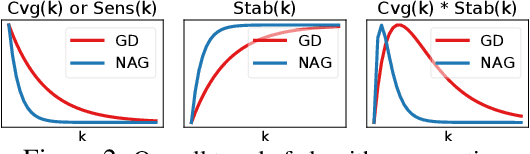
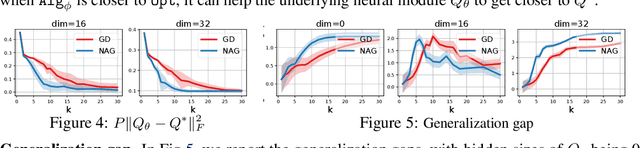
Abstract:Recently, there has been a surge of interest in combining deep learning models with reasoning in order to handle more sophisticated learning tasks. In many cases, a reasoning task can be solved by an iterative algorithm. This algorithm is often unrolled, and used as a specialized layer in the deep architecture, which can be trained end-to-end with other neural components. Although such hybrid deep architectures have led to many empirical successes, the theoretical foundation of such architectures, especially the interplay between algorithm layers and other neural layers, remains largely unexplored. In this paper, we take an initial step towards an understanding of such hybrid deep architectures by showing that properties of the algorithm layers, such as convergence, stability, and sensitivity, are intimately related to the approximation and generalization abilities of the end-to-end model. Furthermore, our analysis matches closely our experimental observations under various conditions, suggesting that our theory can provide useful guidelines for designing deep architectures with reasoning layers.
Learning to Stop While Learning to Predict
Jun 09, 2020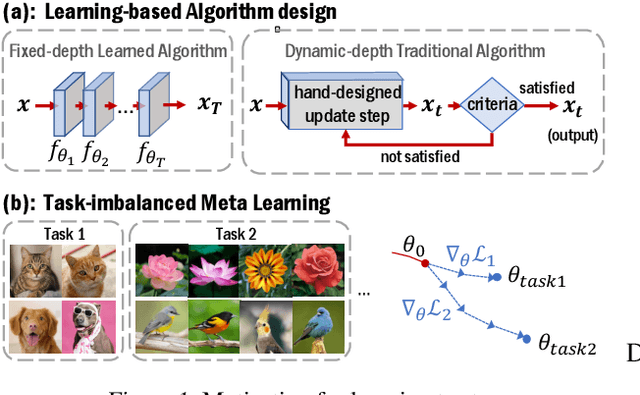

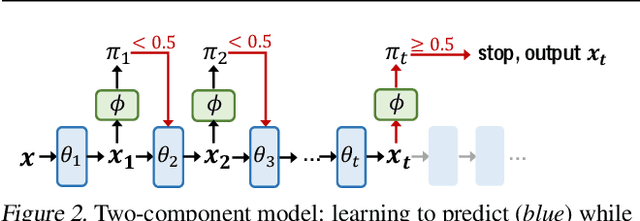
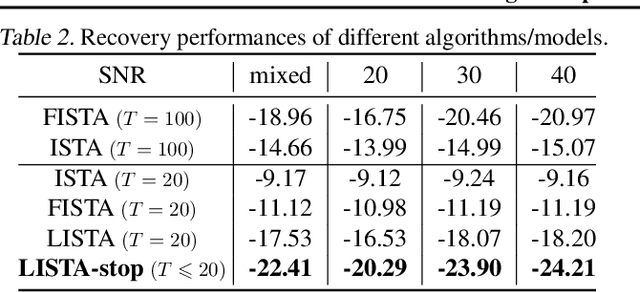
Abstract:There is a recent surge of interest in designing deep architectures based on the update steps in traditional algorithms, or learning neural networks to improve and replace traditional algorithms. While traditional algorithms have certain stopping criteria for outputting results at different iterations, many algorithm-inspired deep models are restricted to a ``fixed-depth'' for all inputs. Similar to algorithms, the optimal depth of a deep architecture may be different for different input instances, either to avoid ``over-thinking'', or because we want to compute less for operations converged already. In this paper, we tackle this varying depth problem using a steerable architecture, where a feed-forward deep model and a variational stopping policy are learned together to sequentially determine the optimal number of layers for each input instance. Training such architecture is very challenging. We provide a variational Bayes perspective and design a novel and effective training procedure which decomposes the task into an oracle model learning stage and an imitation stage. Experimentally, we show that the learned deep model along with the stopping policy improves the performances on a diverse set of tasks, including learning sparse recovery, few-shot meta learning, and computer vision tasks.
RNA Secondary Structure Prediction By Learning Unrolled Algorithms
Feb 13, 2020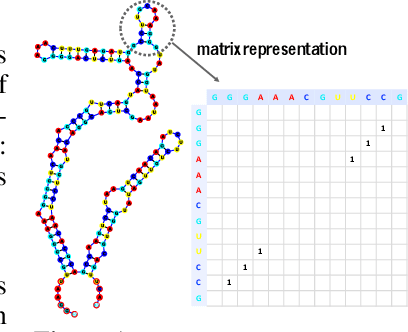
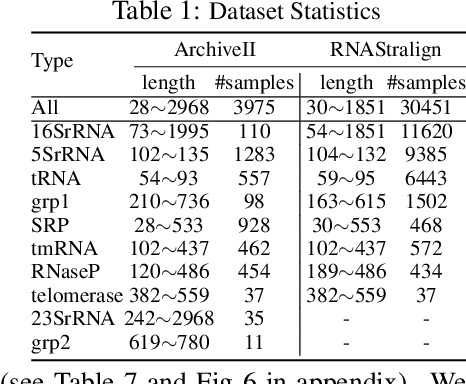
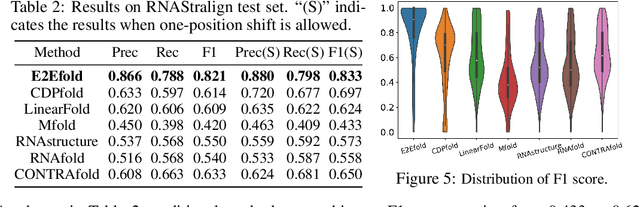
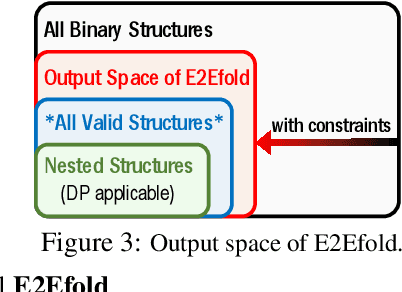
Abstract:In this paper, we propose an end-to-end deep learning model, called E2Efold, for RNA secondary structure prediction which can effectively take into account the inherent constraints in the problem. The key idea of E2Efold is to directly predict the RNA base-pairing matrix, and use an unrolled algorithm for constrained programming as the template for deep architectures to enforce constraints. With comprehensive experiments on benchmark datasets, we demonstrate the superior performance of E2Efold: it predicts significantly better structures compared to previous SOTA (especially for pseudoknotted structures), while being as efficient as the fastest algorithms in terms of inference time.
Efficient Probabilistic Logic Reasoning with Graph Neural Networks
Feb 04, 2020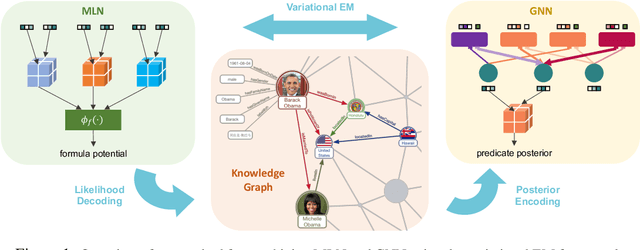
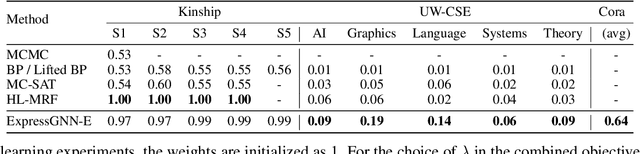
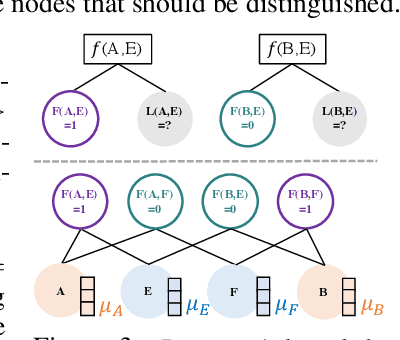
Abstract:Markov Logic Networks (MLNs), which elegantly combine logic rules and probabilistic graphical models, can be used to address many knowledge graph problems. However, inference in MLN is computationally intensive, making the industrial-scale application of MLN very difficult. In recent years, graph neural networks (GNNs) have emerged as efficient and effective tools for large-scale graph problems. Nevertheless, GNNs do not explicitly incorporate prior logic rules into the models, and may require many labeled examples for a target task. In this paper, we explore the combination of MLNs and GNNs, and use graph neural networks for variational inference in MLN. We propose a GNN variant, named ExpressGNN, which strikes a nice balance between the representation power and the simplicity of the model. Our extensive experiments on several benchmark datasets demonstrate that ExpressGNN leads to effective and efficient probabilistic logic reasoning.
Review: Ordinary Differential Equations For Deep Learning
Nov 01, 2019
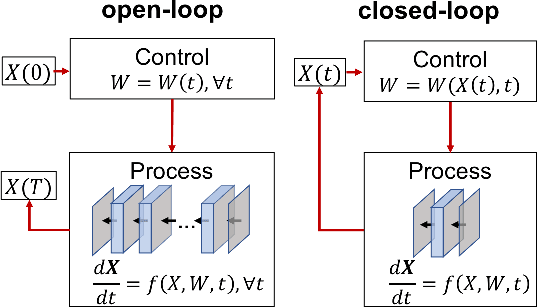


Abstract:To better understand and improve the behavior of neural networks, a recent line of works bridged the connection between ordinary differential equations (ODEs) and deep neural networks (DNNs). The connections are made in two folds: (1) View DNN as ODE discretization; (2) View the training of DNN as solving an optimal control problem. The former connection motivates people either to design neural architectures based on ODE discretization schemes or to replace DNN by a continuous model characterized by ODEs. Several works demonstrated distinct advantages of using a continuous model instead of traditional DNN in some specific applications. The latter connection is inspiring. Based on Pontryagin's maximum principle, which is popular in the optimal control literature, some developed new optimization methods for training neural networks and some developed algorithms to train the infinite-deep continuous model with low memory-cost. This paper is organized as follows: In Section 2, the relation between neural architecture and ODE discretization is introduced. Some architectures are not motivated by ODE, but they are later found to be associated with some specific discretization schemes. Some architectures are designed based on ODE discretization and expected to achieve some special properties. Section 3 formulates the optimization problem where a traditional neural network is replaced by a continuous model (ODE). The formulated optimization problem is an optimal control problem. Therefore, two different types of controls will also be discussed in this section. In Section 4, we will discuss how we can utilize the optimization methods that are popular in optimal control literature to help the training of machine learning problems. Finally, two applications of using a continuous model will be shown in Section 5 and 6 to demonstrate some of its advantages over traditional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge