Patient-Specific Models of Treatment Effects Explain Heterogeneity in Tuberculosis

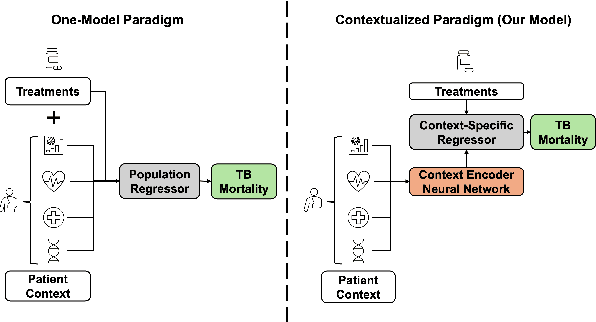
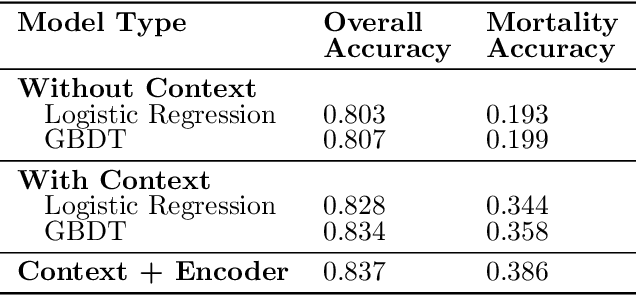
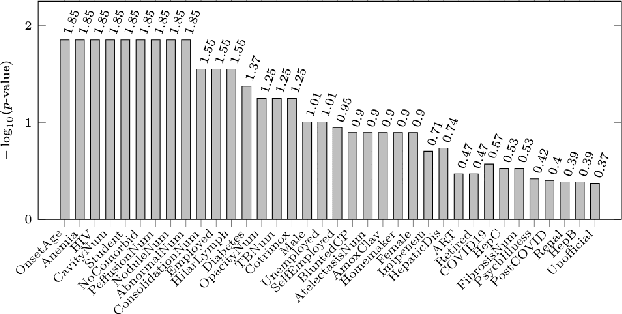
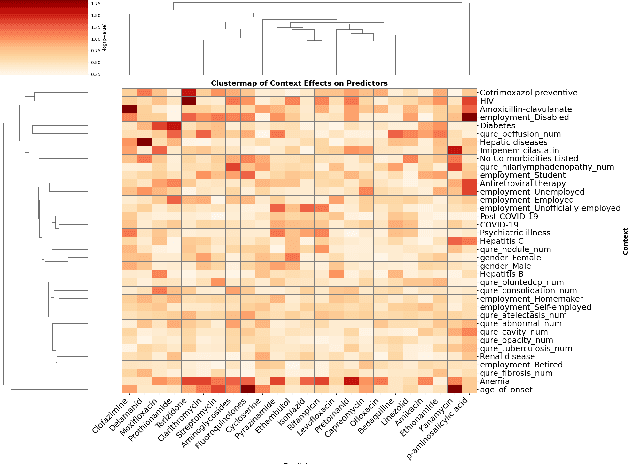
Tuberculosis (TB) is a major global health challenge, and is compounded by co-morbidities such as HIV, diabetes, and anemia, which complicate treatment outcomes and contribute to heterogeneous patient responses. Traditional models of TB often overlook this heterogeneity by focusing on broad, pre-defined patient groups, thereby missing the nuanced effects of individual patient contexts. We propose moving beyond coarse subgroup analyses by using contextualized modeling, a multi-task learning approach that encodes patient context into personalized models of treatment effects, revealing patient-specific treatment benefits. Applied to the TB Portals dataset with multi-modal measurements for over 3,000 TB patients, our model reveals structured interactions between co-morbidities, treatments, and patient outcomes, identifying anemia, age of onset, and HIV as influential for treatment efficacy. By enhancing predictive accuracy in heterogeneous populations and providing patient-specific insights, contextualized models promise to enable new approaches to personalized treatment.

Multi-task Learning of Order-Consistent Causal Graphs

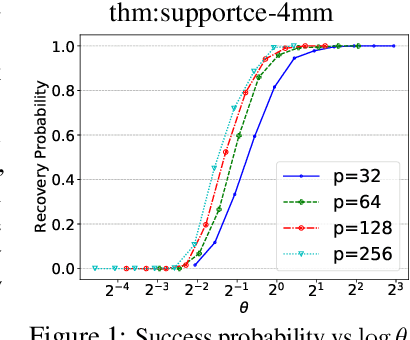
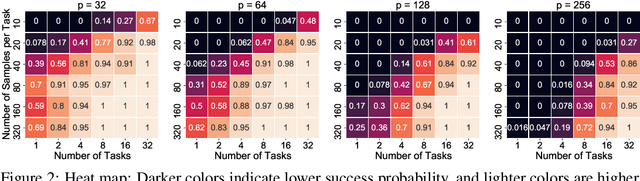
We consider the problem of discovering $K$ related Gaussian directed acyclic graphs (DAGs), where the involved graph structures share a consistent causal order and sparse unions of supports. Under the multi-task learning setting, we propose a $l_1/l_2$-regularized maximum likelihood estimator (MLE) for learning $K$ linear structural equation models. We theoretically show that the joint estimator, by leveraging data across related tasks, can achieve a better sample complexity for recovering the causal order (or topological order) than separate estimations. Moreover, the joint estimator is able to recover non-identifiable DAGs, by estimating them together with some identifiable DAGs. Lastly, our analysis also shows the consistency of union support recovery of the structures. To allow practical implementation, we design a continuous optimization problem whose optimizer is the same as the joint estimator and can be approximated efficiently by an iterative algorithm. We validate the theoretical analysis and the effectiveness of the joint estimator in experiments.

NOTMAD: Estimating Bayesian Networks with Sample-Specific Structures and Parameters

Context-specific Bayesian networks (i.e. directed acyclic graphs, DAGs) identify context-dependent relationships between variables, but the non-convexity induced by the acyclicity requirement makes it difficult to share information between context-specific estimators (e.g. with graph generator functions). For this reason, existing methods for inferring context-specific Bayesian networks have favored breaking datasets into subsamples, limiting statistical power and resolution, and preventing the use of multidimensional and latent contexts. To overcome this challenge, we propose NOTEARS-optimized Mixtures of Archetypal DAGs (NOTMAD). NOTMAD models context-specific Bayesian networks as the output of a function which learns to mix archetypal networks according to sample context. The archetypal networks are estimated jointly with the context-specific networks and do not require any prior knowledge. We encode the acyclicity constraint as a smooth regularization loss which is back-propagated to the mixing function; in this way, NOTMAD shares information between context-specific acyclic graphs, enabling the estimation of Bayesian network structures and parameters at even single-sample resolution. We demonstrate the utility of NOTMAD and sample-specific network inference through analysis and experiments, including patient-specific gene expression networks which correspond to morphological variation in cancer.