Understanding Deep Architectures with Reasoning Layer
Paper and Code
Jun 24, 2020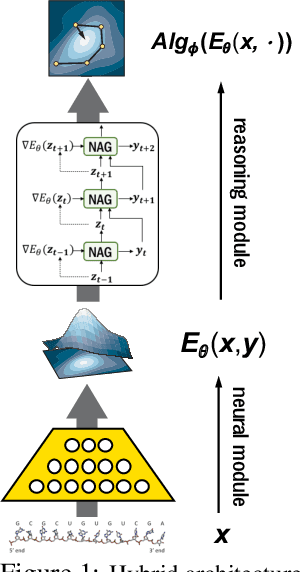

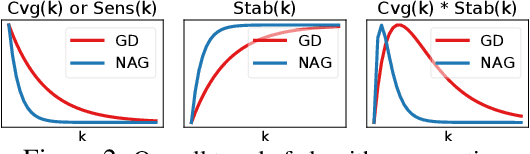
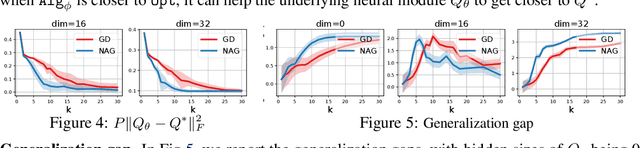
Recently, there has been a surge of interest in combining deep learning models with reasoning in order to handle more sophisticated learning tasks. In many cases, a reasoning task can be solved by an iterative algorithm. This algorithm is often unrolled, and used as a specialized layer in the deep architecture, which can be trained end-to-end with other neural components. Although such hybrid deep architectures have led to many empirical successes, the theoretical foundation of such architectures, especially the interplay between algorithm layers and other neural layers, remains largely unexplored. In this paper, we take an initial step towards an understanding of such hybrid deep architectures by showing that properties of the algorithm layers, such as convergence, stability, and sensitivity, are intimately related to the approximation and generalization abilities of the end-to-end model. Furthermore, our analysis matches closely our experimental observations under various conditions, suggesting that our theory can provide useful guidelines for designing deep architectures with reasoning layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge