Christoph Reisinger
Weighted Conditional Flow Matching
Jul 29, 2025Abstract:Conditional flow matching (CFM) has emerged as a powerful framework for training continuous normalizing flows due to its computational efficiency and effectiveness. However, standard CFM often produces paths that deviate significantly from straight-line interpolations between prior and target distributions, making generation slower and less accurate due to the need for fine discretization at inference. Recent methods enhance CFM performance by inducing shorter and straighter trajectories but typically rely on computationally expensive mini-batch optimal transport (OT). Drawing insights from entropic optimal transport (EOT), we propose Weighted Conditional Flow Matching (W-CFM), a novel approach that modifies the classical CFM loss by weighting each training pair $(x, y)$ with a Gibbs kernel. We show that this weighting recovers the entropic OT coupling up to some bias in the marginals, and we provide the conditions under which the marginals remain nearly unchanged. Moreover, we establish an equivalence between W-CFM and the minibatch OT method in the large-batch limit, showing how our method overcomes computational and performance bottlenecks linked to batch size. Empirically, we test our method on unconditional generation on various synthetic and real datasets, confirming that W-CFM achieves comparable or superior sample quality, fidelity, and diversity to other alternative baselines while maintaining the computational efficiency of vanilla CFM.
Efficient Learning for Entropy-regularized Markov Decision Processes via Multilevel Monte Carlo
Mar 27, 2025
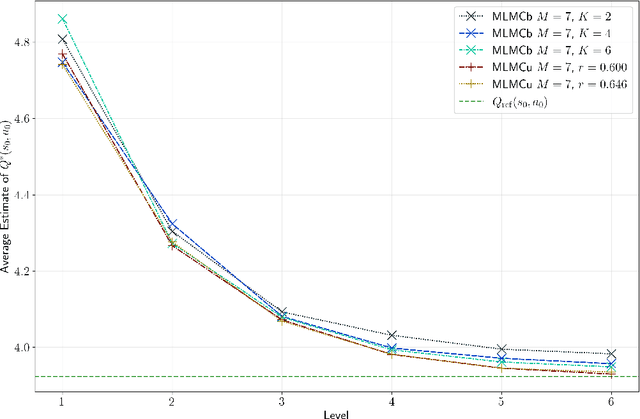
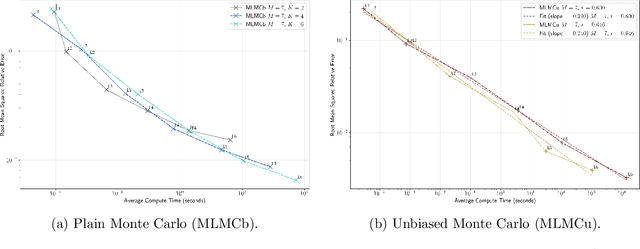
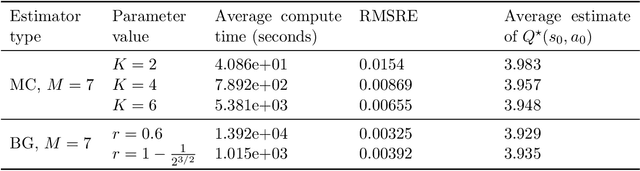
Abstract:Designing efficient learning algorithms with complexity guarantees for Markov decision processes (MDPs) with large or continuous state and action spaces remains a fundamental challenge. We address this challenge for entropy-regularized MDPs with Polish state and action spaces, assuming access to a generative model of the environment. We propose a novel family of multilevel Monte Carlo (MLMC) algorithms that integrate fixed-point iteration with MLMC techniques and a generic stochastic approximation of the Bellman operator. We quantify the precise impact of the chosen approximate Bellman operator on the accuracy of the resulting MLMC estimator. Leveraging this error analysis, we show that using a biased plain MC estimate for the Bellman operator results in quasi-polynomial sample complexity, whereas an unbiased randomized multilevel approximation of the Bellman operator achieves polynomial sample complexity in expectation. Notably, these complexity bounds are independent of the dimensions or cardinalities of the state and action spaces, distinguishing our approach from existing algorithms whose complexities scale with the sizes of these spaces. We validate these theoretical performance guarantees through numerical experiments.
Limit Order Book Simulation and Trade Evaluation with $K$-Nearest-Neighbor Resampling
Sep 10, 2024



Abstract:In this paper, we show how $K$-nearest neighbor ($K$-NN) resampling, an off-policy evaluation method proposed in \cite{giegrich2023k}, can be applied to simulate limit order book (LOB) markets and how it can be used to evaluate and calibrate trading strategies. Using historical LOB data, we demonstrate that our simulation method is capable of recreating realistic LOB dynamics and that synthetic trading within the simulation leads to a market impact in line with the corresponding literature. Compared to other statistical LOB simulation methods, our algorithm has theoretical convergence guarantees under general conditions, does not require optimization, is easy to implement and computationally efficient. Furthermore, we show that in a benchmark comparison our method outperforms a deep learning-based algorithm for several key statistics. In the context of a LOB with pro-rata type matching, we demonstrate how our algorithm can calibrate the size of limit orders for a liquidation strategy. Finally, we describe how $K$-NN resampling can be modified for choices of higher dimensional state spaces.
$K$-Nearest-Neighbor Resampling for Off-Policy Evaluation in Stochastic Control
Jun 07, 2023


Abstract:We propose a novel $K$-nearest neighbor resampling procedure for estimating the performance of a policy from historical data containing realized episodes of a decision process generated under a different policy. We focus on feedback policies that depend deterministically on the current state in environments with continuous state-action spaces and system-inherent stochasticity effected by chosen actions. Such settings are common in a wide range of high-stake applications and are actively investigated in the context of stochastic control. Our procedure exploits that similar state/action pairs (in a metric sense) are associated with similar rewards and state transitions. This enables our resampling procedure to tackle the counterfactual estimation problem underlying off-policy evaluation (OPE) by simulating trajectories similarly to Monte Carlo methods. Compared to other OPE methods, our algorithm does not require optimization, can be efficiently implemented via tree-based nearest neighbor search and parallelization and does not explicitly assume a parametric model for the environment's dynamics. These properties make the proposed resampling algorithm particularly useful for stochastic control environments. We prove that our method is statistically consistent in estimating the performance of a policy in the OPE setting under weak assumptions and for data sets containing entire episodes rather than independent transitions. To establish the consistency, we generalize Stone's Theorem, a well-known result in nonparametric statistics on local averaging, to include episodic data and the counterfactual estimation underlying OPE. Numerical experiments demonstrate the effectiveness of the algorithm in a variety of stochastic control settings including a linear quadratic regulator, trade execution in limit order books and online stochastic bin packing.
Convergence of policy gradient methods for finite-horizon stochastic linear-quadratic control problems
Nov 01, 2022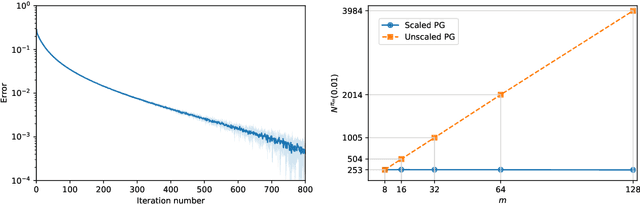
Abstract:We study the global linear convergence of policy gradient (PG) methods for finite-horizon exploratory linear-quadratic control (LQC) problems. The setting includes stochastic LQC problems with indefinite costs and allows additional entropy regularisers in the objective. We consider a continuous-time Gaussian policy whose mean is linear in the state variable and whose covariance is state-independent. Contrary to discrete-time problems, the cost is noncoercive in the policy and not all descent directions lead to bounded iterates. We propose geometry-aware gradient descents for the mean and covariance of the policy using the Fisher geometry and the Bures-Wasserstein geometry, respectively. The policy iterates are shown to satisfy an a-priori bound, and converge globally to the optimal policy with a linear rate. We further propose a novel PG method with discrete-time policies. The algorithm leverages the continuous-time analysis, and achieves a robust linear convergence across different action frequencies. A numerical experiment confirms the convergence and robustness of the proposed algorithm.
Hedging option books using neural-SDE market models
May 31, 2022



Abstract:We study the capability of arbitrage-free neural-SDE market models to yield effective strategies for hedging options. In particular, we derive sensitivity-based and minimum-variance-based hedging strategies using these models and examine their performance when applied to various option portfolios using real-world data. Through backtesting analysis over typical and stressed market periods, we show that neural-SDE market models achieve lower hedging errors than Black--Scholes delta and delta-vega hedging consistently over time, and are less sensitive to the tenor choice of hedging instruments. In addition, hedging using market models leads to similar performance to hedging using Heston models, while the former tends to be more robust during stressed market periods.
Linear convergence of a policy gradient method for finite horizon continuous time stochastic control problems
Mar 22, 2022Abstract:Despite its popularity in the reinforcement learning community, a provably convergent policy gradient method for general continuous space-time stochastic control problems has been elusive. This paper closes the gap by proposing a proximal gradient algorithm for feedback controls of finite-time horizon stochastic control problems. The state dynamics are continuous time nonlinear diffusions with controlled drift and possibly degenerate noise, and the objectives are nonconvex in the state and nonsmooth in the control. We prove under suitable conditions that the algorithm converges linearly to a stationary point of the control problem, and is stable with respect to policy updates by approximate gradient steps. The convergence result justifies the recent reinforcement learning heuristics that adding entropy regularization to the optimization objective accelerates the convergence of policy gradient methods. The proof exploits careful regularity estimates of backward stochastic differential equations.
Estimating risks of option books using neural-SDE market models
Feb 15, 2022Abstract:In this paper, we examine the capacity of an arbitrage-free neural-SDE market model to produce realistic scenarios for the joint dynamics of multiple European options on a single underlying. We subsequently demonstrate its use as a risk simulation engine for option portfolios. Through backtesting analysis, we show that our models are more computationally efficient and accurate for evaluating the Value-at-Risk (VaR) of option portfolios, with better coverage performance and less procyclicality than standard filtered historical simulation approaches.
Arbitrage-free neural-SDE market models
May 24, 2021Abstract:Modelling joint dynamics of liquid vanilla options is crucial for arbitrage-free pricing of illiquid derivatives and managing risks of option trade books. This paper develops a nonparametric model for the European options book respecting underlying financial constraints and while being practically implementable. We derive a state space for prices which are free from static (or model-independent) arbitrage and study the inference problem where a model is learnt from discrete time series data of stock and option prices. We use neural networks as function approximators for the drift and diffusion of the modelled SDE system, and impose constraints on the neural nets such that no-arbitrage conditions are preserved. In particular, we give methods to calibrate \textit{neural SDE} models which are guaranteed to satisfy a set of linear inequalities. We validate our approach with numerical experiments using data generated from a Heston stochastic local volatility model.
Understanding Deep Architectures with Reasoning Layer
Jun 24, 2020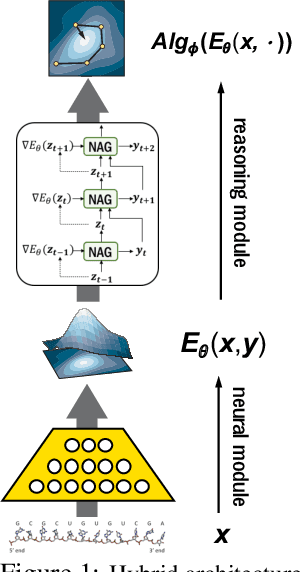

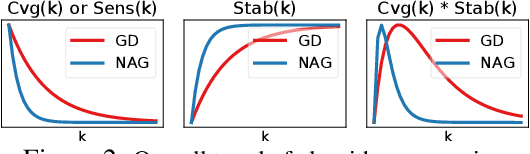
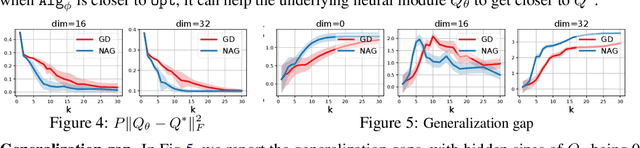
Abstract:Recently, there has been a surge of interest in combining deep learning models with reasoning in order to handle more sophisticated learning tasks. In many cases, a reasoning task can be solved by an iterative algorithm. This algorithm is often unrolled, and used as a specialized layer in the deep architecture, which can be trained end-to-end with other neural components. Although such hybrid deep architectures have led to many empirical successes, the theoretical foundation of such architectures, especially the interplay between algorithm layers and other neural layers, remains largely unexplored. In this paper, we take an initial step towards an understanding of such hybrid deep architectures by showing that properties of the algorithm layers, such as convergence, stability, and sensitivity, are intimately related to the approximation and generalization abilities of the end-to-end model. Furthermore, our analysis matches closely our experimental observations under various conditions, suggesting that our theory can provide useful guidelines for designing deep architectures with reasoning layers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge