Limit Order Book Simulation and Trade Evaluation with $K$-Nearest-Neighbor Resampling

In this paper, we show how $K$-nearest neighbor ($K$-NN) resampling, an off-policy evaluation method proposed in \cite{giegrich2023k}, can be applied to simulate limit order book (LOB) markets and how it can be used to evaluate and calibrate trading strategies. Using historical LOB data, we demonstrate that our simulation method is capable of recreating realistic LOB dynamics and that synthetic trading within the simulation leads to a market impact in line with the corresponding literature. Compared to other statistical LOB simulation methods, our algorithm has theoretical convergence guarantees under general conditions, does not require optimization, is easy to implement and computationally efficient. Furthermore, we show that in a benchmark comparison our method outperforms a deep learning-based algorithm for several key statistics. In the context of a LOB with pro-rata type matching, we demonstrate how our algorithm can calibrate the size of limit orders for a liquidation strategy. Finally, we describe how $K$-NN resampling can be modified for choices of higher dimensional state spaces.

$K$-Nearest-Neighbor Resampling for Off-Policy Evaluation in Stochastic Control

We propose a novel $K$-nearest neighbor resampling procedure for estimating the performance of a policy from historical data containing realized episodes of a decision process generated under a different policy. We focus on feedback policies that depend deterministically on the current state in environments with continuous state-action spaces and system-inherent stochasticity effected by chosen actions. Such settings are common in a wide range of high-stake applications and are actively investigated in the context of stochastic control. Our procedure exploits that similar state/action pairs (in a metric sense) are associated with similar rewards and state transitions. This enables our resampling procedure to tackle the counterfactual estimation problem underlying off-policy evaluation (OPE) by simulating trajectories similarly to Monte Carlo methods. Compared to other OPE methods, our algorithm does not require optimization, can be efficiently implemented via tree-based nearest neighbor search and parallelization and does not explicitly assume a parametric model for the environment's dynamics. These properties make the proposed resampling algorithm particularly useful for stochastic control environments. We prove that our method is statistically consistent in estimating the performance of a policy in the OPE setting under weak assumptions and for data sets containing entire episodes rather than independent transitions. To establish the consistency, we generalize Stone's Theorem, a well-known result in nonparametric statistics on local averaging, to include episodic data and the counterfactual estimation underlying OPE. Numerical experiments demonstrate the effectiveness of the algorithm in a variety of stochastic control settings including a linear quadratic regulator, trade execution in limit order books and online stochastic bin packing.

Convergence of policy gradient methods for finite-horizon stochastic linear-quadratic control problems

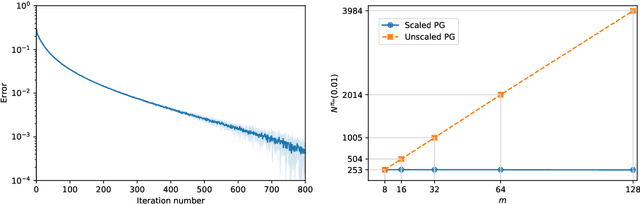
We study the global linear convergence of policy gradient (PG) methods for finite-horizon exploratory linear-quadratic control (LQC) problems. The setting includes stochastic LQC problems with indefinite costs and allows additional entropy regularisers in the objective. We consider a continuous-time Gaussian policy whose mean is linear in the state variable and whose covariance is state-independent. Contrary to discrete-time problems, the cost is noncoercive in the policy and not all descent directions lead to bounded iterates. We propose geometry-aware gradient descents for the mean and covariance of the policy using the Fisher geometry and the Bures-Wasserstein geometry, respectively. The policy iterates are shown to satisfy an a-priori bound, and converge globally to the optimal policy with a linear rate. We further propose a novel PG method with discrete-time policies. The algorithm leverages the continuous-time analysis, and achieves a robust linear convergence across different action frequencies. A numerical experiment confirms the convergence and robustness of the proposed algorithm.