An Offline Learning Approach to Propagator Models

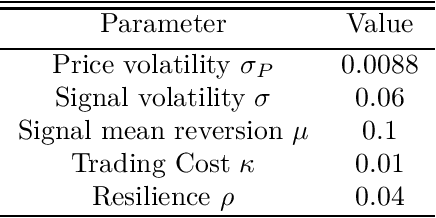
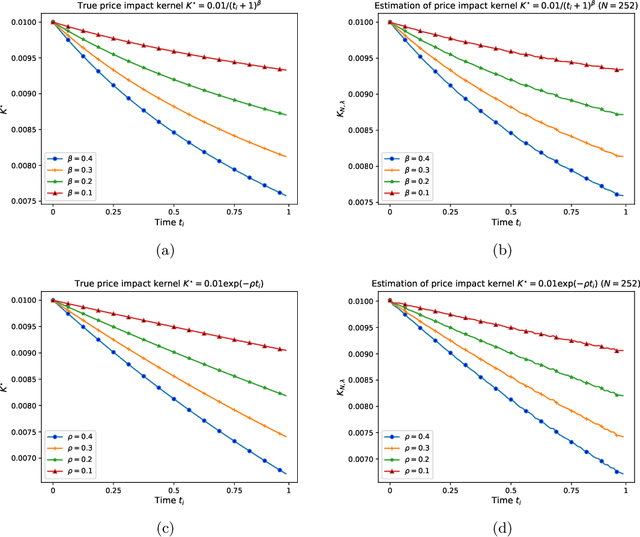
We consider an offline learning problem for an agent who first estimates an unknown price impact kernel from a static dataset, and then designs strategies to liquidate a risky asset while creating transient price impact. We propose a novel approach for a nonparametric estimation of the propagator from a dataset containing correlated price trajectories, trading signals and metaorders. We quantify the accuracy of the estimated propagator using a metric which depends explicitly on the dataset. We show that a trader who tries to minimise her execution costs by using a greedy strategy purely based on the estimated propagator will encounter suboptimality due to so-called spurious correlation between the trading strategy and the estimator and due to intrinsic uncertainty resulting from a biased cost functional. By adopting an offline reinforcement learning approach, we introduce a pessimistic loss functional taking the uncertainty of the estimated propagator into account, with an optimiser which eliminates the spurious correlation, and derive an asymptotically optimal bound on the execution costs even without precise information on the true propagator. Numerical experiments are included to demonstrate the effectiveness of the proposed propagator estimator and the pessimistic trading strategy.

Linear convergence of a policy gradient method for finite horizon continuous time stochastic control problems

Despite its popularity in the reinforcement learning community, a provably convergent policy gradient method for general continuous space-time stochastic control problems has been elusive. This paper closes the gap by proposing a proximal gradient algorithm for feedback controls of finite-time horizon stochastic control problems. The state dynamics are continuous time nonlinear diffusions with controlled drift and possibly degenerate noise, and the objectives are nonconvex in the state and nonsmooth in the control. We prove under suitable conditions that the algorithm converges linearly to a stationary point of the control problem, and is stable with respect to policy updates by approximate gradient steps. The convergence result justifies the recent reinforcement learning heuristics that adding entropy regularization to the optimization objective accelerates the convergence of policy gradient methods. The proof exploits careful regularity estimates of backward stochastic differential equations.