Review: Ordinary Differential Equations For Deep Learning
Paper and Code
Nov 01, 2019
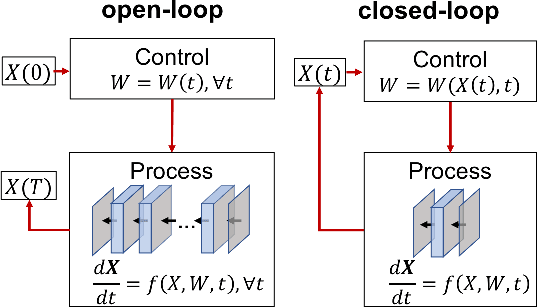


To better understand and improve the behavior of neural networks, a recent line of works bridged the connection between ordinary differential equations (ODEs) and deep neural networks (DNNs). The connections are made in two folds: (1) View DNN as ODE discretization; (2) View the training of DNN as solving an optimal control problem. The former connection motivates people either to design neural architectures based on ODE discretization schemes or to replace DNN by a continuous model characterized by ODEs. Several works demonstrated distinct advantages of using a continuous model instead of traditional DNN in some specific applications. The latter connection is inspiring. Based on Pontryagin's maximum principle, which is popular in the optimal control literature, some developed new optimization methods for training neural networks and some developed algorithms to train the infinite-deep continuous model with low memory-cost. This paper is organized as follows: In Section 2, the relation between neural architecture and ODE discretization is introduced. Some architectures are not motivated by ODE, but they are later found to be associated with some specific discretization schemes. Some architectures are designed based on ODE discretization and expected to achieve some special properties. Section 3 formulates the optimization problem where a traditional neural network is replaced by a continuous model (ODE). The formulated optimization problem is an optimal control problem. Therefore, two different types of controls will also be discussed in this section. In Section 4, we will discuss how we can utilize the optimization methods that are popular in optimal control literature to help the training of machine learning problems. Finally, two applications of using a continuous model will be shown in Section 5 and 6 to demonstrate some of its advantages over traditional neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge