uGLAD: Sparse graph recovery by optimizing deep unrolled networks

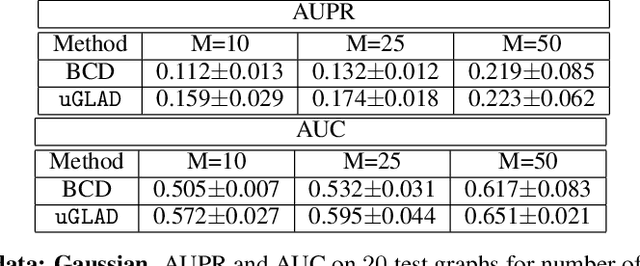
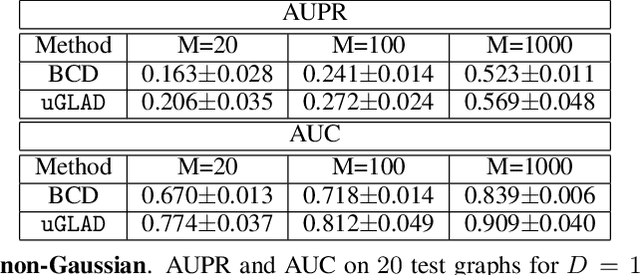
Probabilistic Graphical Models (PGMs) are generative models of complex systems. They rely on conditional independence assumptions between variables to learn sparse representations which can be visualized in a form of a graph. Such models are used for domain exploration and structure discovery in poorly understood domains. This work introduces a novel technique to perform sparse graph recovery by optimizing deep unrolled networks. Assuming that the input data $X\in\mathbb{R}^{M\times D}$ comes from an underlying multivariate Gaussian distribution, we apply a deep model on $X$ that outputs the precision matrix $\Theta$, which can also be interpreted as the adjacency matrix. Our model, uGLAD, builds upon and extends the state-of-the-art model GLAD to the unsupervised setting. The key benefits of our model are (1) uGLAD automatically optimizes sparsity-related regularization parameters leading to better performance than existing algorithms. (2) We introduce multi-task learning based `consensus' strategy for robust handling of missing data in an unsupervised setting. We evaluate model results on synthetic Gaussian data, non-Gaussian data generated from Gene Regulatory Networks, and present a case study in anaerobic digestion.