Generative Kaleidoscopic Networks
Paper and Code
Feb 27, 2024
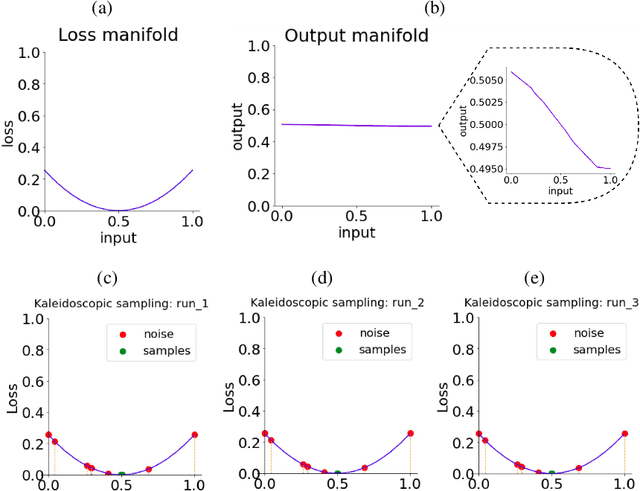
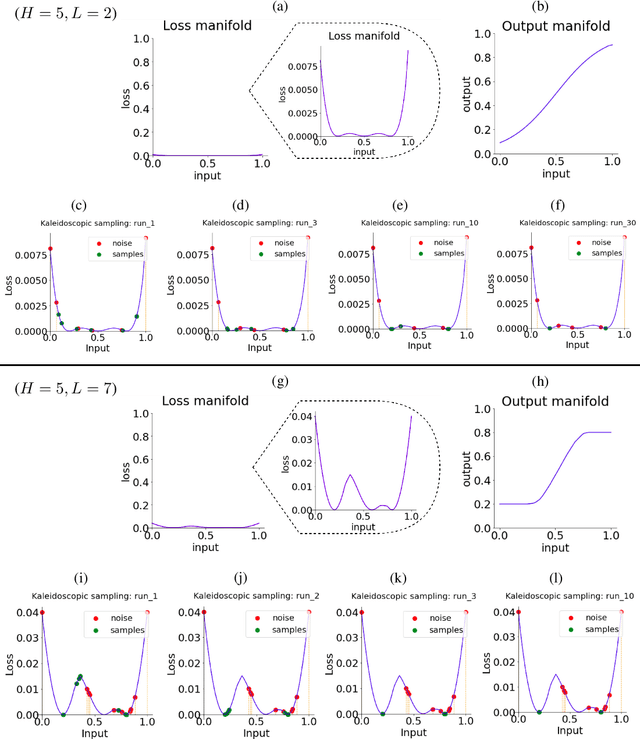
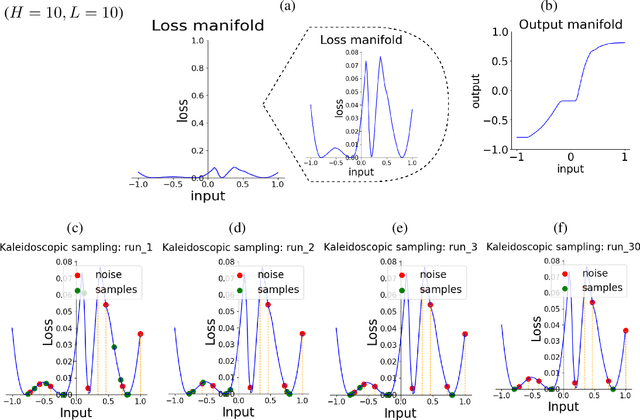
We discovered that the neural networks, especially the deep ReLU networks, demonstrate an `over-generalization' phenomenon. That is, the output values for the inputs that were not seen during training are mapped close to the output range that were observed during the learning process. In other words, the neural networks learn a many-to-one mapping and this effect is more prominent as we increase the number of layers or the depth of the neural network. We utilize this property of neural networks to design a dataset kaleidoscope, termed as `Generative Kaleidoscopic Networks'. Briefly, if we learn a model to map from input $x\in\mathbb{R}^D$ to itself $f_\mathcal{N}(x)\rightarrow x$, the proposed `Kaleidoscopic sampling' procedure starts with a random input noise $z\in\mathbb{R}^D$ and recursively applies $f_\mathcal{N}(\cdots f_\mathcal{N}(z)\cdots )$. After a burn-in period duration, we start observing samples from the input distribution and the quality of samples recovered improves as we increase the depth of the model. Scope: We observed this phenomenon to various degrees for the other deep learning architectures like CNNs, Transformers & U-Nets and we are currently investigating them further.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge