On the Whitney extension problem for near isometries and beyond
Paper and Code
Mar 17, 2021

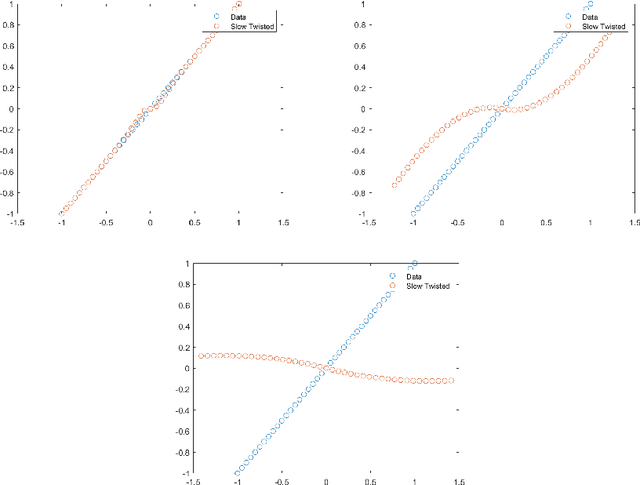
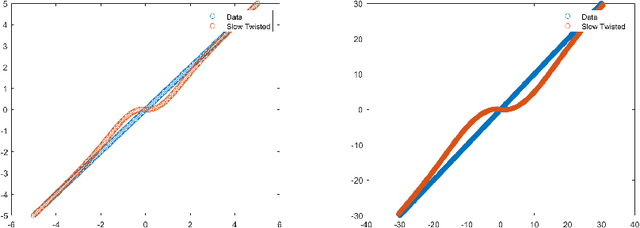
This paper is an exposition of work of the author et al. detailing fascinating connections between several mathematical problems which lie on the intersection of several mathematics subjects, namely algebraic-differential geometry, analysis on manifolds, complex-harmonic analysis, data science, partial differential equations, optimization and probability. A significant portion of the work is based on joint research with Charles Fefferman in the papers [39, 40, 41, 42]. The topics of this work include (a) The space of maps of bounded mean oscillation (BMO) in $\mathbb R^D,\, D\geq 2$. (b) The labeled and unlabeled near alignment and Procrustes problem for point sets with certain geometries and for not too thin compact sets both in $\mathbb R^D,\, D\geq 2$. (c) The Whitney near isometry extension problem for point sets with certain geometries and for not too thin compact sets both in $\mathbb R^D,\, D\geq 2$. (d) Partitions and clustering of compact sets and point sets with certain geometries in $\mathbb R^D,\, D\geq 2$ and analysis on certain manifolds in $\mathbb R^D,\, D\geq 2$. Many open problems for future research are given.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge