Ayfer Ozgur
Leveraging Randomness in Model and Data Partitioning for Privacy Amplification
Mar 04, 2025Abstract:We study how inherent randomness in the training process -- where each sample (or client in federated learning) contributes only to a randomly selected portion of training -- can be leveraged for privacy amplification. This includes (1) data partitioning, where a sample participates in only a subset of training iterations, and (2) model partitioning, where a sample updates only a subset of the model parameters. We apply our framework to model parallelism in federated learning, where each client updates a randomly selected subnetwork to reduce memory and computational overhead, and show that existing methods, e.g. model splitting or dropout, provide a significant privacy amplification gain not captured by previous privacy analysis techniques. Additionally, we introduce Balanced Iteration Subsampling, a new data partitioning method where each sample (or client) participates in a fixed number of training iterations. We show that this method yields stronger privacy amplification than Poisson (i.i.d.) sampling of data (or clients). Our results demonstrate that randomness in the training process, which is structured rather than i.i.d. and interacts with data in complex ways, can be systematically leveraged for significant privacy amplification.
Exact Optimality of Communication-Privacy-Utility Tradeoffs in Distributed Mean Estimation
Jun 08, 2023

Abstract:We study the mean estimation problem under communication and local differential privacy constraints. While previous work has proposed \emph{order}-optimal algorithms for the same problem (i.e., asymptotically optimal as we spend more bits), \emph{exact} optimality (in the non-asymptotic setting) still has not been achieved. In this work, we take a step towards characterizing the \emph{exact}-optimal approach in the presence of shared randomness (a random variable shared between the server and the user) and identify several necessary conditions for \emph{exact} optimality. We prove that one of the necessary conditions is to utilize a rotationally symmetric shared random codebook. Based on this, we propose a randomization mechanism where the codebook is a randomly rotated simplex -- satisfying the necessary properties of the \emph{exact}-optimal codebook. The proposed mechanism is based on a $k$-closest encoding which we prove to be \emph{exact}-optimal for the randomly rotated simplex codebook.
Privacy Amplification via Compression: Achieving the Optimal Privacy-Accuracy-Communication Trade-off in Distributed Mean Estimation
Apr 04, 2023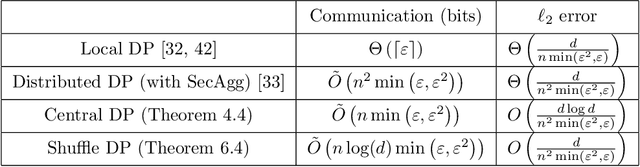
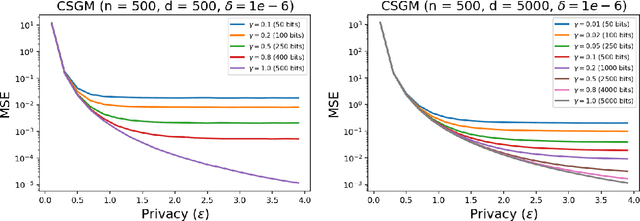
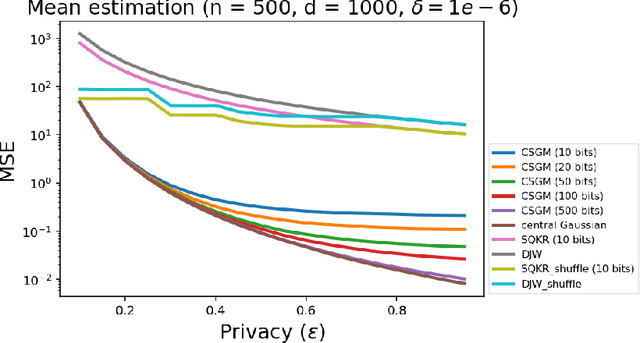
Abstract:Privacy and communication constraints are two major bottlenecks in federated learning (FL) and analytics (FA). We study the optimal accuracy of mean and frequency estimation (canonical models for FL and FA respectively) under joint communication and $(\varepsilon, \delta)$-differential privacy (DP) constraints. We show that in order to achieve the optimal error under $(\varepsilon, \delta)$-DP, it is sufficient for each client to send $\Theta\left( n \min\left(\varepsilon, \varepsilon^2\right)\right)$ bits for FL and $\Theta\left(\log\left( n\min\left(\varepsilon, \varepsilon^2\right) \right)\right)$ bits for FA to the server, where $n$ is the number of participating clients. Without compression, each client needs $O(d)$ bits and $\log d$ bits for the mean and frequency estimation problems respectively (where $d$ corresponds to the number of trainable parameters in FL or the domain size in FA), which means that we can get significant savings in the regime $ n \min\left(\varepsilon, \varepsilon^2\right) = o(d)$, which is often the relevant regime in practice. Our algorithms leverage compression for privacy amplification: when each client communicates only partial information about its sample, we show that privacy can be amplified by randomly selecting the part contributed by each client.
Understanding Entropic Regularization in GANs
Nov 02, 2021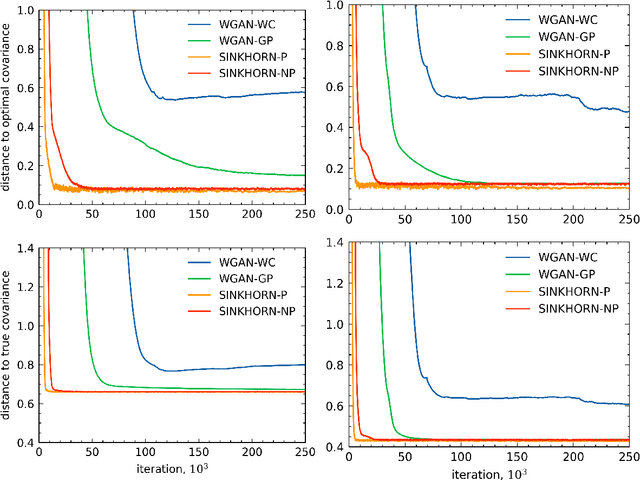
Abstract:Generative Adversarial Networks are a popular method for learning distributions from data by modeling the target distribution as a function of a known distribution. The function, often referred to as the generator, is optimized to minimize a chosen distance measure between the generated and target distributions. One commonly used measure for this purpose is the Wasserstein distance. However, Wasserstein distance is hard to compute and optimize, and in practice entropic regularization techniques are used to improve numerical convergence. The influence of regularization on the learned solution, however, remains not well-understood. In this paper, we study how several popular entropic regularizations of Wasserstein distance impact the solution in a simple benchmark setting where the generator is linear and the target distribution is high-dimensional Gaussian. We show that entropy regularization promotes the solution sparsification, while replacing the Wasserstein distance with the Sinkhorn divergence recovers the unregularized solution. Both regularization techniques remove the curse of dimensionality suffered by Wasserstein distance. We show that the optimal generator can be learned to accuracy $\epsilon$ with $O(1/\epsilon^2)$ samples from the target distribution. We thus conclude that these regularization techniques can improve the quality of the generator learned from empirical data for a large class of distributions.
Batched Thompson Sampling
Oct 01, 2021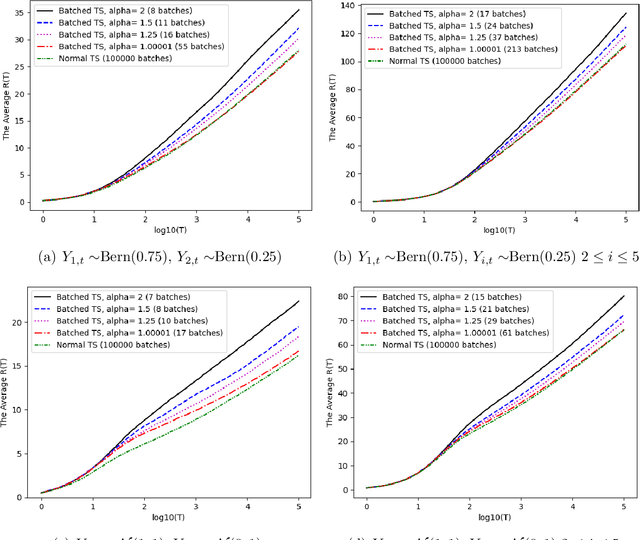
Abstract:We introduce a novel anytime Batched Thompson sampling policy for multi-armed bandits where the agent observes the rewards of her actions and adjusts her policy only at the end of a small number of batches. We show that this policy simultaneously achieves a problem dependent regret of order $O(\log(T))$ and a minimax regret of order $O(\sqrt{T\log(T)})$ while the number of batches can be bounded by $O(\log(T))$ independent of the problem instance over a time horizon $T$. We also show that in expectation the number of batches used by our policy can be bounded by an instance dependent bound of order $O(\log\log(T))$. These results indicate that Thompson sampling maintains the same performance in this batched setting as in the case when instantaneous feedback is available after each action, while requiring minimal feedback. These results also indicate that Thompson sampling performs competitively with recently proposed algorithms tailored for the batched setting. These algorithms optimize the batch structure for a given time horizon $T$ and prioritize exploration in the beginning of the experiment to eliminate suboptimal actions. We show that Thompson sampling combined with an adaptive batching strategy can achieve a similar performance without knowing the time horizon $T$ of the problem and without having to carefully optimize the batch structure to achieve a target regret bound (i.e. problem dependent vs minimax regret) for a given $T$.
Asymptotic Performance of Thompson Sampling in the Batched Multi-Armed Bandits
Oct 01, 2021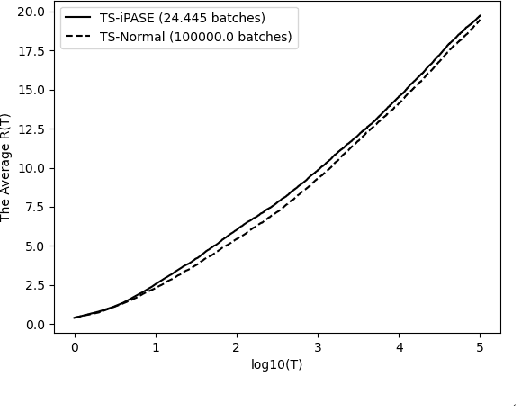
Abstract:We study the asymptotic performance of the Thompson sampling algorithm in the batched multi-armed bandit setting where the time horizon $T$ is divided into batches, and the agent is not able to observe the rewards of her actions until the end of each batch. We show that in this batched setting, Thompson sampling achieves the same asymptotic performance as in the case where instantaneous feedback is available after each action, provided that the batch sizes increase subexponentially. This result implies that Thompson sampling can maintain its performance even if it receives delayed feedback in $\omega(\log T)$ batches. We further propose an adaptive batching scheme that reduces the number of batches to $\Theta(\log T)$ while maintaining the same performance. Although the batched multi-armed bandit setting has been considered in several recent works, previous results rely on tailored algorithms for the batched setting, which optimize the batch structure and prioritize exploration in the beginning of the experiment to eliminate suboptimal actions. We show that Thompson sampling, on the other hand, is able to achieve a similar asymptotic performance in the batched setting without any modifications.
* This work was presented in 2021 IEEE International Symposium on Information Theory (ISIT)
Over-the-Air Statistical Estimation
Mar 06, 2021Abstract:We study schemes and lower bounds for distributed minimax statistical estimation over a Gaussian multiple-access channel (MAC) under squared error loss, in a framework combining statistical estimation and wireless communication. First, we develop "analog" joint estimation-communication schemes that exploit the superposition property of the Gaussian MAC and we characterize their risk in terms of the number of nodes and dimension of the parameter space. Then, we derive information-theoretic lower bounds on the minimax risk of any estimation scheme restricted to communicate the samples over a given number of uses of the channel and show that the risk achieved by our proposed schemes is within a logarithmic factor of these lower bounds. We compare both achievability and lower bound results to previous "digital" lower bounds, where nodes transmit errorless bits at the Shannon capacity of the MAC, showing that estimation schemes that leverage the physical layer offer a drastic reduction in estimation error over digital schemes relying on a physical-layer abstraction.
Asymptotic Convergence of Thompson Sampling
Nov 08, 2020Abstract:Thompson sampling has been shown to be an effective policy across a variety of online learning tasks. Many works have analyzed the finite time performance of Thompson sampling, and proved that it achieves a sub-linear regret under a broad range of probabilistic settings. However its asymptotic behavior remains mostly underexplored. In this paper, we prove an asymptotic convergence result for Thompson sampling under the assumption of a sub-linear Bayesian regret, and show that the actions of a Thompson sampling agent provide a strongly consistent estimator of the optimal action. Our results rely on the martingale structure inherent in Thompson sampling.
Information Constrained Optimal Transport: From Talagrand, to Marton, to Cover
Aug 24, 2020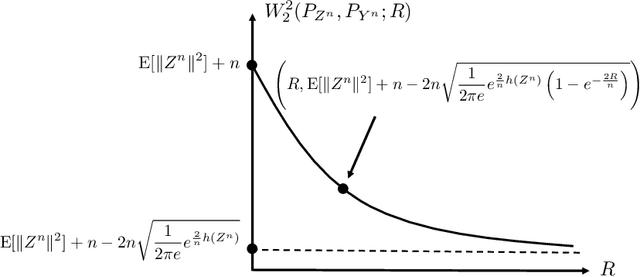
Abstract:The optimal transport problem studies how to transport one measure to another in the most cost-effective way and has wide range of applications from economics to machine learning. In this paper, we introduce and study an information constrained variation of this problem. Our study yields a strengthening and generalization of Talagrand's celebrated transportation cost inequality. Following Marton's approach, we show that the new transportation cost inequality can be used to recover old and new concentration of measure results. Finally, we provide an application of this new inequality to network information theory. We show that it can be used to recover almost immediately a recent solution to a long-standing open problem posed by Cover regarding the capacity of the relay channel.
Global Multiclass Classification from Heterogeneous Local Models
May 25, 2020
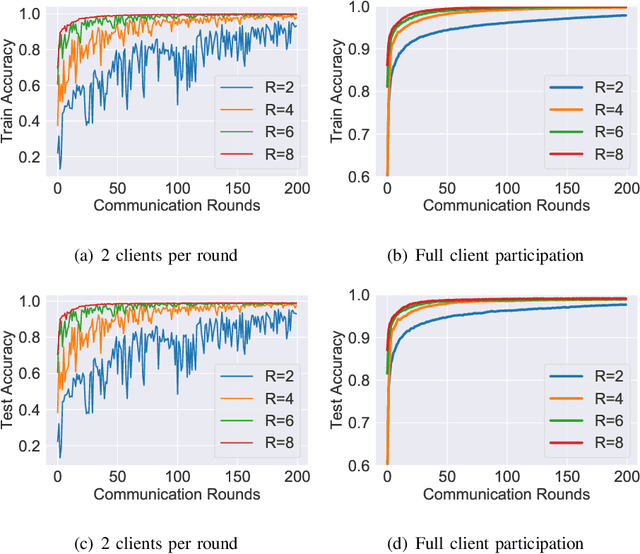
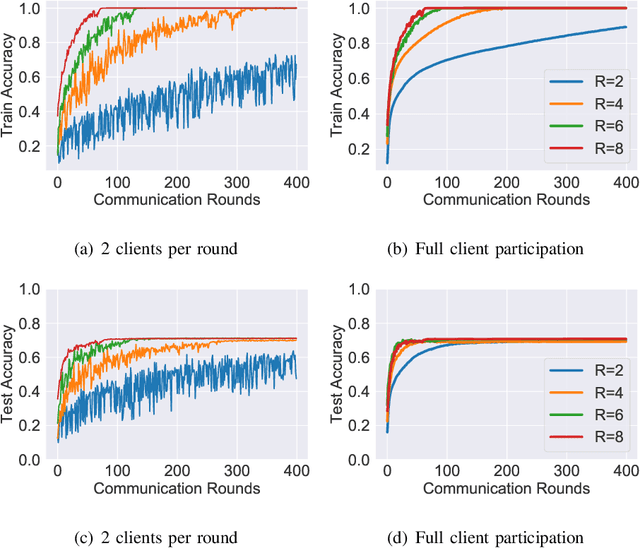
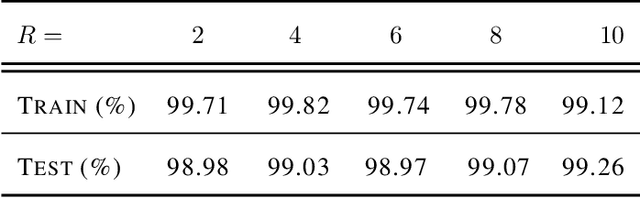
Abstract:Multiclass classification problems are most often solved by either training a single centralized classifier on all $K$ classes, or by reducing the problem to multiple binary classification tasks. This paper explores the uncharted region between these two extremes: How can we solve the $K$-class classification problem by combining the predictions of smaller classifiers, each trained on an arbitrary number of classes $R \in \{2, 3, \ldots, K\}$? We present a mathematical framework for answering this question, and derive bounds on the number of classifiers (in terms of $K$ and $R$) needed to accurately predict the true class of an unlabeled sample under both adversarial and stochastic assumptions. By exploiting a connection to the classical set cover problem in combinatorics, we produce an efficient, near-optimal scheme (with respect to the number of classifiers) for designing such configurations of classifiers, which recovers the well-known one-vs.-one strategy as a special case when $R=2$. Experiments with the MNIST and CIFAR-10 datasets show that our scheme is capable of matching the performance of centralized classifiers in practice. The results suggest that our approach offers a promising direction for solving the problem of data heterogeneity which plagues current federated learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge