Global Multiclass Classification from Heterogeneous Local Models
Paper and Code
May 25, 2020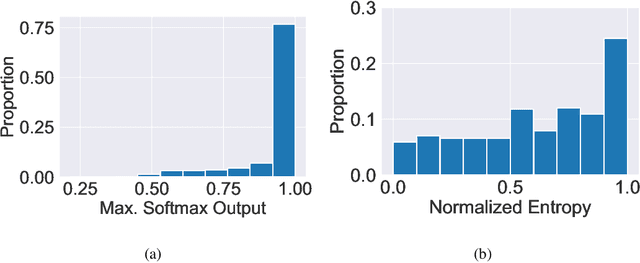
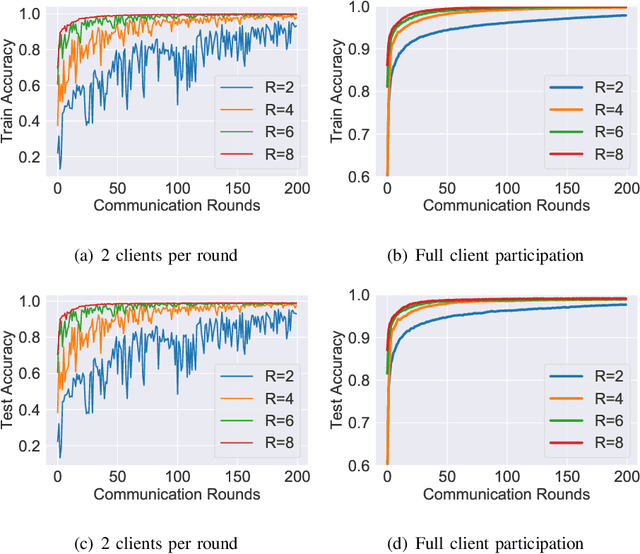
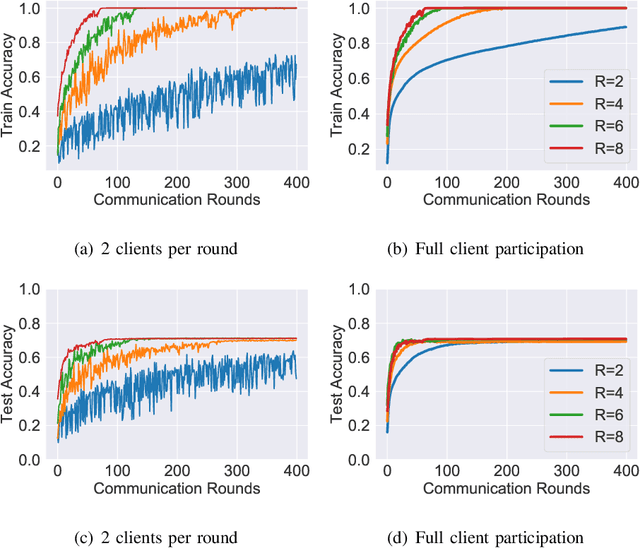
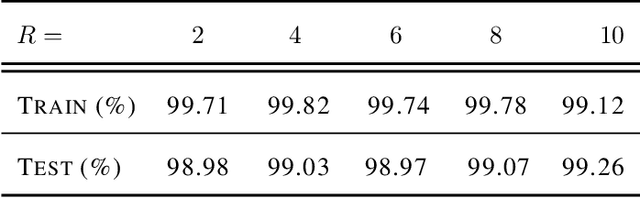
Multiclass classification problems are most often solved by either training a single centralized classifier on all $K$ classes, or by reducing the problem to multiple binary classification tasks. This paper explores the uncharted region between these two extremes: How can we solve the $K$-class classification problem by combining the predictions of smaller classifiers, each trained on an arbitrary number of classes $R \in \{2, 3, \ldots, K\}$? We present a mathematical framework for answering this question, and derive bounds on the number of classifiers (in terms of $K$ and $R$) needed to accurately predict the true class of an unlabeled sample under both adversarial and stochastic assumptions. By exploiting a connection to the classical set cover problem in combinatorics, we produce an efficient, near-optimal scheme (with respect to the number of classifiers) for designing such configurations of classifiers, which recovers the well-known one-vs.-one strategy as a special case when $R=2$. Experiments with the MNIST and CIFAR-10 datasets show that our scheme is capable of matching the performance of centralized classifiers in practice. The results suggest that our approach offers a promising direction for solving the problem of data heterogeneity which plagues current federated learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge