Asymptotic Performance of Thompson Sampling in the Batched Multi-Armed Bandits

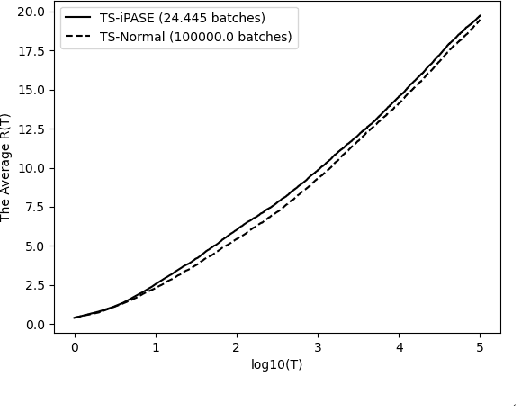
We study the asymptotic performance of the Thompson sampling algorithm in the batched multi-armed bandit setting where the time horizon $T$ is divided into batches, and the agent is not able to observe the rewards of her actions until the end of each batch. We show that in this batched setting, Thompson sampling achieves the same asymptotic performance as in the case where instantaneous feedback is available after each action, provided that the batch sizes increase subexponentially. This result implies that Thompson sampling can maintain its performance even if it receives delayed feedback in $\omega(\log T)$ batches. We further propose an adaptive batching scheme that reduces the number of batches to $\Theta(\log T)$ while maintaining the same performance. Although the batched multi-armed bandit setting has been considered in several recent works, previous results rely on tailored algorithms for the batched setting, which optimize the batch structure and prioritize exploration in the beginning of the experiment to eliminate suboptimal actions. We show that Thompson sampling, on the other hand, is able to achieve a similar asymptotic performance in the batched setting without any modifications.